Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.5 - Ex. 48
Use o roteiro desta seção para esboçar a curva
Passo 1
Oiee, vamos começar resolvendo essa questãozinha?
Primeiro, determinamos o domínio da função
- O logaritmo natural, está definido apenas para
- Portanto, o domínio da função é
Vamos verificar a simetria da função para poder simplificar o esboço da curva.
- A função não é definida para então não faz sentido verificar simetria par ou ímpar.
Passo 2
Analisamos o comportamento da função para valores extremos de (quando e
- Para
À medida que
- Para
Quando
No entanto, como está se aproximando de , o produto também tende a 0, pois se aproxima mais rapidamente de .
Passo 3
Calculamos a derivada para entender o comportamento monótono da função.
Usamos a regra do produto e a regra da cadeia para derivar:
Analisamos os pontos críticos onde
Portanto, ou
- implica
- implica
Passo 4
Analisamos o sinal da derivada em torno desses pontos críticos:
- Para
A função é crescente.
- Para
A função é decrescente.
- Para
A função é crescente.
Portanto:
- é um ponto de máximo local.
- é um ponto de mínimo local.
A função não cruza o eixo y porque não está definida para
Passo 5
Para o gráfico
- A função tem um domínio em
- A função é crescente para , decrescente para e crescente para
- Máximo local em
- Mínimo local em
Calculamos o valor da função nos pontos críticos:
- Para
- Para
Passo 6
Pontos para Esboço
-
-
Com base nas análises acima, podemos esboçar a curva da função
- A função começa em valores muito pequenos quando próximo de 0 e cresce até
- Decresce para entre e , atingindo o mínimo local em .
- Cresce novamente para tendendo a infinito à medida que
O gráfico da função será assim:
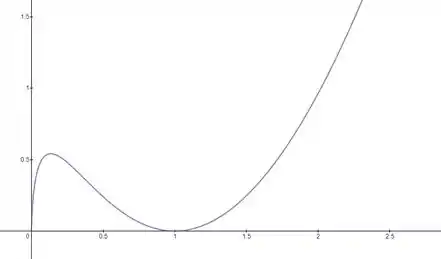
Resposta
Vide o passo a passo.