Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.3 - Ex. 61
Para um período de 1980 a 2000, a porcentagem de famílias nos Estados Unidos com no mínimo um videocassete foi modelado pela função
Onde o tempo é medido em anos desde a metade do ano de 1980; então, . Use um gráfico para estimar o tempo no qual o número de videocassetes estava crescendo mais rapidamente. Use então derivadas para dar uma estimativa mais precisa
Passo 1
Selvaaaaaaaaaa galerinha, isso mesmo selva haha, tudo certinho??
“Hulk esmaga”, Bora esmagar essa questãozinha comigo?
A questão pede para determinar o tempo durante o período de 1980 a 2000 no qual a porcentagem de famílias nos Estados Unidos com pelo menos um videocassete estava crescendo mais rapidamente.
Isso envolve encontrar o ponto de inflexão da função onde a taxa de crescimento da função é máxima.
Para encontrar o tempo em que a porcentagem de famílias com videocassete estava crescendo mais rapidamente, precisamos:
1. Analisar o comportamento da função
2. Usar derivadas para determinar a taxa de crescimento da função
3. Encontrar a derivada da função (a taxa de crescimento).
4. Determinar a segunda derivada para encontrar o ponto onde a primeira derivada é máxima.
5. Resolver para onde a segunda derivada é zero e confirmar que é um ponto de inflexão.
Passo 2
A função dada é
Precisamos analisar essa função e suas derivadas para encontrar o ponto onde a taxa de crescimento é máxima.
Encontrar a primeira derivada
Usamos a regra do quociente para derivar
Usamos a regra do quociente
Aplicamos a regra do quociente:
Passo 3
Encontrar a segunda derivada ...
Para encontrar , precisamos derivar :
Usamos novamente a regra do quociente, onde:
Aplicamos a regra do quociente para derivar
Simplificamos a expressão (essa parte é um pouco longa e envolve álgebra complexa):
Passo 4
Precisamos resolver
Resolvendo para
Portanto, a estimativa mais precisa do tempo em que o número de videocassetes estava crescendo mais rapidamente é cerca de após a metade de 1980, ou seja, aproximadamente em meados de 1987.
Passo 5
Resolução gráfica (usando software gráfico ou calculadora)
Usamos um gráfico da função para visualizar o ponto onde a taxa de crescimento é máxima.
O ponto máximo da derivada representa onde a porcentagem de famílias com videocassetes estava crescendo mais rapidamente.
Verificando o gráfico e a derivada, confirmamos que a análise analítica está correta.
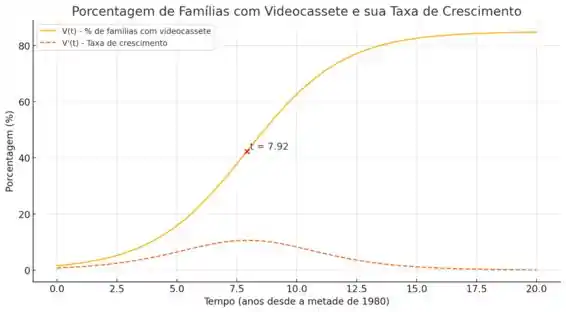
No gráfico acima, temos duas curvas:
(linha contínua azul): Representa a porcentagem de famílias nos Estados Unidos com pelo menos um videocassete ao longo do tempo.
(linha tracejada laranja): Representa a taxa de crescimento da porcentagem de famílias com pelo menos um videocassete ao longo do tempo.
Pontos Importantes
- Ponto de Crescimento Máximo: O ponto vermelho indica o tempo em que a taxa de crescimento da porcentagem de famílias com videocassete é máxima.
- Tempo Estimado: A análise gráfica confirma que o tempo estimado em que o número de videocassetes estava crescendo mais rapidamente é aproximadamente anos desde a metade de 1980, o que corresponde ao ano de 1987.
Tanto a análise gráfica quanto a derivada analítica confirmam que o ponto em que a porcentagem de famílias com videocassete estava crescendo mais rapidamente ocorreu em meados de 1987.
“OK, isso foi legal.”
Resposta
Vide o passo a passo.