Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.3 - Ex. 30
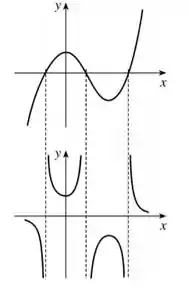
Use o gráfico dado de para esboçar o gráfico . Quais aspectos de são os mais importantes no esboço de ? Explique como eles são usados.
Passo 1
E aí galerinha, como estão?
Essa questão aqui é sobre gráficos de funções! Vamos ver como transformar o gráfico de dado no enunciado no gráfico de . Preparados? Bora lá!
Temos que ver quais características de são as mais importantes para o nosso desenho.
Iremos ter dois tipos de ponto em especial: os pontos que cortam o eixo e os pontos de máximo e mínimo, beleza?
Esses pontos costumam ser importante quando a gente vai construir ou analisar qualquer gráfico, então sempre vai logo desconfiando deles!
Outro aspecto importante: reparar quando a função cresce e quando ela decresce.
Perceba que e são inversamente proporcionais, ou seja: quando um cresce, o outro decresce.
Se for um valor muuuito grande, vai ser um valor beeem pequeno, beleza? Podemos tirar a seguinte conclusão: os pontos de máximo de serão pontos de mínimo em , e vice-versa.
Quando estiver crescendo, vai estar decrescendo, combinado?
Veja só! 😁
Passo 2
Temos um detalhe muuuuuuito importante que devemos reparar: temos uma restrição no domínio de , a de que (não existe divisão por zero!). No pontos onde for zero, não vai existir , teremos só uma assíntota vertical, fechou?
Bora lá! 😎
Passo 3
Bora relembrar o que a gente descobriu: pontos de máximo em são pontos de mínimo em , e vice-versa. Onde cresce, decresce e vice-versa. Por último, onde é zerp, terá uma assíntota vertical, beleza? Olha só como vai ficar o nosso gráfico! O de cima é o que tínhamos e o de baixo é o que encontramos:
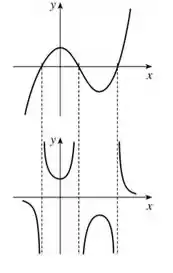
E aí! o que achou? Responde Aí! 👀
Resposta
Os aspectos mais importante são: os pontos de máximo, mínimo e de zero em , além de verificar onde ele cresce e decresce. Esses aspecto irão mostrar o crescimento e decrescimento de , além de pontos de máximo, mínimo e pontos onde a função não existe. O gráfico de e comparados são os da figura abaixo:
