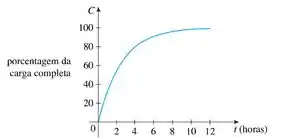
Uma pilha recarregável é colocada no carregador. O gráfico mostra , a porcentagem de capacidade total que a pilha alcança como uma função do tempo decorrido (em horas).

(a) Qual o significado da derivada ?(b) Esboce o gráfico de . O que o gráfico diz?

Para fazer o item (a), precisamos lembrar o que a derivada de uma função representa.

É sempre útil tentar enxergar a derivada como a taxa de variação da função. Mas o que isso significa?

Nesse caso, a função que estamos observando é a porcentagem da carga da pilha, certo? Então podemos dizer que a derivada dessa função consiste em quão rápido essa pilha está carregando a cada instante de tempo .

Pegou a ideia? 🙂

Agora para fecharmos o item (b) temos que esboçar o gráfico de .

Pra fazermos isso, lembramos que a derivada tem pode ser vista como a inclinação da reta tangente e estimamos os seus valores usando essas retas. Pra ilustrar, vamos marcar algumas dessas retas no nosso gráfico:

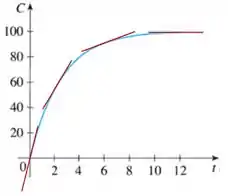
Lembre-se que queremos apenas fazer um esboço, então não precisamos de valores exatos, apenas um entendimento de como a derivada evolui com o tempo. Pela figura, fazemos as seguintes observações:

Em , a reta crescente é crescente. Isso significa o que a derivada é positiva nesse ponto.

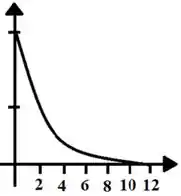
As inclinações ficam cada vez menores conforme o tempo passa até finalmente chegar a uma reta horizontal no final. Então podemos dizer que a derivada diminui até assumir o valor zero.

Os valores das inclinações caem rapidamente no início, mas depois começam a diminuir lentamente enquanto se aproximam de zero. Esse comportamento sugere que o gráfico de terá concavidade pra cima.

Juntando essas informações, temos o seguinte:

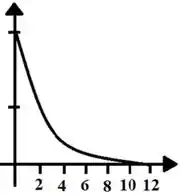
O gráfico de nos diz que a taxa de variação percentual da capacidade total está diminuindo e se aproximando de .

É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍