Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.5 - Ex. 29
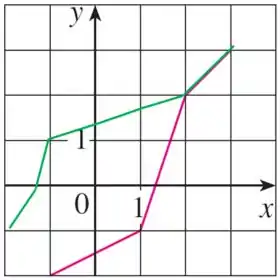
Use o gráfico dado de para esboçar .
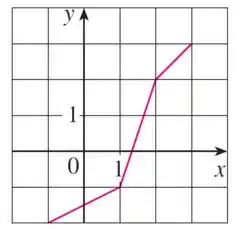
Passo 1
Opa, a questão nos dá o gráfico:
E pede pra a gente esboçar !
Bom, o gráfico de uma função inversa é a reflexão em torno da bissetriz da .
Tá, mas o que é a bissetriz?Nada mais é do que uma reta de 45º que passa pela origem. Algo assim:
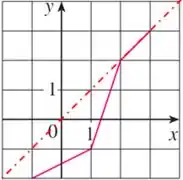
Então, tudo o que temos que fazer é imaginar essa reflexão! Para isso basta imaginar que a reta é um espelho e você precisa espelhar a função de um lado para o outro do espelho.
Passo 2
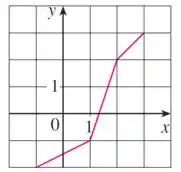
Para ajudar a refletir, vamos traçar alguns pontos na função e então traçar aonde esses pontos estariam refletidos do outro lado da bissetriz:
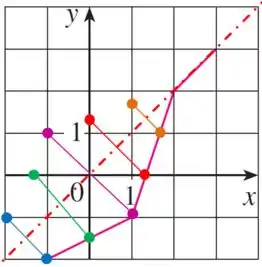
O que pode te ajudar a traçar esses pontos refletidos é:
1. A distância de um ponto da função até a bissetriz é igual a distância do ponto do lado refletido até a bissetriz.
2. Um ponto que está no eixo terá seu ponto refletido no eixo , e um ponto que está no eixo terá seu ponto refletido no eixo .
3. A distância horizontal de um ponto em relação ao eixo é igual a distância vertical do seu ponto refletido em relação ao eixo . E a distância vertical de um ponto em relação ao eixo é igual a distância horizontal do seu ponto refletido em relação ao eixo .
Ou seja, quando refletimos pela bissetriz tudo que é horizontal vira vertical e tudo que é vertical vira horizontal.
Passo 3
Agora vamos traçar o gráfico refletido unindo os pontos refletidos.
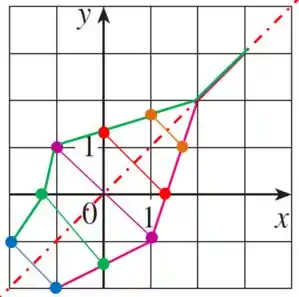
Prontinho! Agora, só pra ficar bonitinho vou tirar os pontos que nos ajudaram e deixar só a função e a função refletida ;)
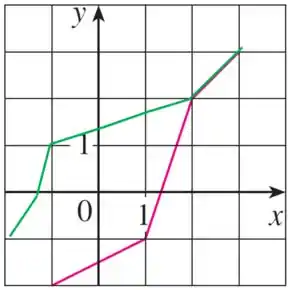
Resposta
