Use os guias desta seção para traçar a curva.
Passo 1
Bom pessoal, nesta seção nos é dado um guia para seguir que ajuda a traçar a curva de uma função. Vamos segui-lo:
- O domínio da função será os reais, já que não há nenhuma restrição na equação.
- Descobrir as interceptações da curva nos eixos y e x. Para x = 0, temos . Para
- Checando simetria:
- Para encontrar assíntotas, temos que checar a existência de limites.
- Intervalos crescentes e decrescentes. Temos que analisar a primeira derivada da função, onde:
- Pontos de máximos e mínimos. Para encontrar estes pontos, temos que conhecer as raízes de e avaliar se há troca de sinal de Ou então avaliar o sinal da segunda derivada nas raízes de
- Para analisar a concavidade da função e achar seus intervalos, devemos usar a segunda derivada da função.
Portanto, não há simetria na função.
Assíntotas Horizontais:
Vamos lá:
Portanto, não temos assíntotas horizontais.
Também não temos assíntotas Verticais, pois o denominador nunca será zero.
Vamos lá:
Crescente:
Decrescente:
Vamos lá:
Na raiz de
Voltando na equação original de f(x):
Pontos de inflexão ocorrem na mudança de concavidade.
Logo, os intervalos são:
H.
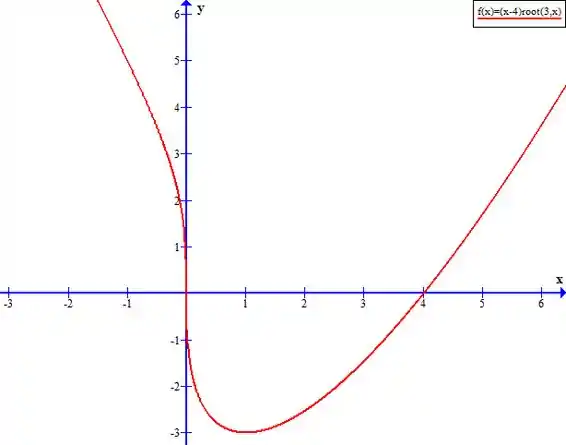
Resposta
Ei, a resposta está no passo a passo :)