Descreva como o gráfico de varia de acordo com a variação de . Faça vários gráficos da família para ilustrar as tendências que você encontrou. Em particular, você deve investigar como os pontos de máximos e mínimos e os pontos de inflexão se movem quando muda. Você também deve identificar valores de transição para c no qual a forma básica da curva muda.

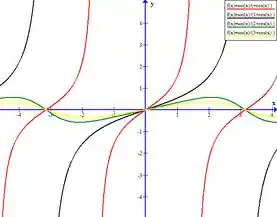
Vamos começar plotando os gráficos de para ... em especial , , e .

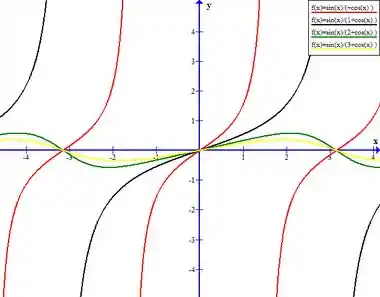
Para vamos plotar , , e ...

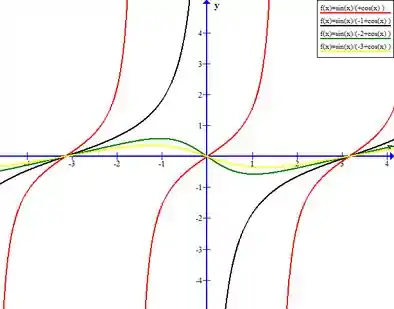
Quando temos o gráfico da tangente, função periódica e ímpar.

Quando o gráfico tende a “deitar”, isto é, fica mais largo em . Os pontos de interseção são periódicos e cruzam o eixo a cada .

E quando Para , não há interceptação no eixo , pois o denominador da função fica igual a zero. Para valores de , os limites somem, pois o denominador não será nunca igual a zero.

Show?

Vamos calcular as derivadas de e ver como impacta...

Vamos calcular a primeira derivada usando a regra do quociente...

Sabemos que , então

Vamos aproveitar e tambem calcular a derivada de segunda ordem de pelo mesmo método...

Nota-se que o termo influencia o comportamento da função, pois os outros valores são sempre positivos (estão elevados ao quadrado).

Os pontos de máximo e mínimo ocorrem quando pois é quando .

A concavidade segue a função seno, ou seja, quando será para cima e quando será para baixo.

Os pontos de inflexão ocorrem quando , ou seja...

Tranquilo até aqui?

Para Há interceptação no eixo quando para todos os valores de . O comportamento da função é quase o mesmo, mas deslocado de para o lado.

Para valores de , os limites ao infinito somem, pois o denominador não será nunca igual a zero. Os pontos de máximo e mínimo continuam a ocorrer quando .

Já as concavidades ficam “invertidas” em relação ao A concavidade segue a função -seno, ou seja, quando será para baixo e quando será para cima.

Os pontos de inflexão continuam quando

É isso! O que achou? Responde Aí!