Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 6.3 - Ex. 3
Use o método das cascas cilíndricas para achar o volume gerado pela rotação em torno do eixo da região limitada pelas curvas dadas. Esboce a região e uma casca típica.
Passo 1
Opa, bora começar com o esboço da região e de uma casca típica de:
Pra começar vamos esboçar a região delimitada pelas curvas acima:
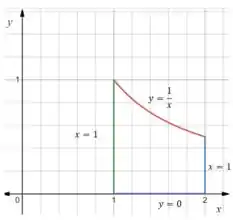
Repara que a altura é igual a :
Aqui a gente vai usar o método das cascas cilíndricas! Fazendo uma rotação em torno do eixo :
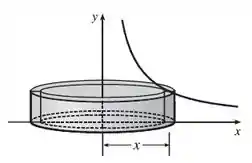
Passo 2
Para calcular o volume usamos a fórmula:
Onde é a circunferência, é a altura e a espessura. Como vimos lá em cima a altura é igual a . Além disso as retas e delimitam a região, então:
Passo 3
Agora precisamos resolver:
Bem, para achar o valor dessa integral vamos calcular a integral indefinida dela e depois utilizamos o Teorema Fundamental do Cálculo para aplicar os limites de integração.
Agora é fácil achar as primitivas da função, usando uma expressão da Tabela de Integrais Indefinidas:
Agora é só aplicar:
Pronto, já encontramos a integral indefinida. Perceba que nem seria necessário colocar a constante de integração nesse caso, pois a gente usou a integral indefinida mais como uma ferramenta para calcular a integral. Agora é só calcular a integral definida usando o Teorema Fundamental do Cálculo:
Vamos lá:
Prontinho!