Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.8 - Ex. 37
Use o m��todo de Newton para encontrar as coordenadas do ponto de inflexão da curva , , com precisão de seis casas decimais.
Passo 1
E aí! tudo certinho?
Nesse problema temos que usar o método de Newton para determinar as coordenadas do ponto de inflexão da curva
No intervalo .
Tem ideia de como fazemos isso?
Vamos lá aplicar o método de Newton, para isso vamos usar sua fórmula, entretanto já que queremos achar o ponto de inflexão de devemos achar os zeros de , então a fórmula fica :
Onde
Sacou? Bora começar!
Passo 2
Vamos começar calculando as derivadas de .
Vamos aplicar a regra da cadeia para obter a derivada de primeira ordem.
E para obter a derivada de segunda ordem vamos aplicar a regra do produto
Show?
Passo 3
Pronto, agora que temos e é só jogar na fórmula de Newton:
Vamos agora analisar qual valor usar para , pelo gráfico de e , vamos usar , pronto, agora é só substituir, vai ser cansativo, mas vamos lá:
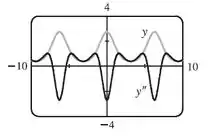
Como queremos uma precisão de seis casas decimais, vamos continuar usando o método de Newton até o valor de deixar de variar, vamos lá:
Mais uma vez, agora com :
Pronto, o valor não varia mais, então a raiz é .
Vamos calcular para ter o ponto de inflexão:
E aí! o que achou? Responde Aí!
Resposta
O ponto de inflexão é .