Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.5 - Ex. 50
Use o roteiro dessa seção para esboçar a curva.
Passo 1
Fala aí! tudo certinho? 😉
Nesse problema vamos usarmos o roteiro de esboço de curvas dado na seção para esboçar o gráfico da função dada por
Para iniciar a questão vamos relembrar um pouco da teoria:
Domínio: Conjunto de todos os valores de para os quais a função é definida.
Interseções com os Eixos:
- Eixo : Onde
- Eixo : Onde ou seja,
Simetria:
- Função Par:
- Função Ímpar:
Assíntotas:
- Assíntotas Verticais: Linhas verticais onde a função cresce sem limites.
- Assíntotas Horizontais: Linhas horizontais que a função se aproxima conforme
Derivadas e Comportamento da Função:
- Primeira Derivada Para determinar onde a função é crescente ou decrescente.
- Segunda Derivada Para determinar a concavidade e pontos de inflexão.
Os intervalos nos quais uma função é crescente (ou decrescente) correspondem aos intervalos nos quais sua derivada é positiva (ou negativa). Então, se quisermos encontrar os intervalos em que uma função é crescente ou decrescente, nós calculamos sua derivada e descobrimos onde ela é positiva ou negativa (o que é mais fácil!).
Concavidade e Pontos de Inflexão:
- Concavidade para cima:
- Concavidade para baixo:
- Pontos de Inflexão: Onde e muda de sinal.
Bora lá!! 😉
Passo 2
A gente precisa lembrar certinho dos passos, em? Se seguir tudo bonitinho todo mundo acha a curva!!
- Primeiro a gente procura o domínio da função.
- Agora procuramos intersecções. Há intersecção com o eixo se for possível encontrar , mas já vimos ali em cima que não pode assumir esse valor então pimba!
- Testando as três possibilidades de simetria:
- Agora tem que lembrar lá do começo como resolve limite, porque vamos procurar as assíntotas.
- Primeiro vamos encontrar os intervalos em que a função cresce ou decresce calculando a derivada primeira:
- Agora é a hora de achar os pontos extremos.
- O último passo antes de montar o gráfico é achar as concavidades e pontos de inflexão, que vamos encontrar calculando a segunda derivada:
Olhando pra ela, vemos que temos na base de uma fração , logo, o único valor que não pode assumir é , portanto, o domínio é .
Passo 3
Não tem intercepto no eixo .
Agora, testamos o do eixo igualando a função a zero, e no nosso caso, não existe, então não há intercepto também!
Passo 4
Já que nenhuma das três possibilidades acontece, não há simetria.
Passo 5
Então bora lá. Temos que
Então é uma assíntota vertical.
Além disso, então, o gráfico se aproxima pela origem quando .
Passo 6
A gente vai entrar agora na parte das derivadas, não pode esquecer em!
Se é maior que zero nesses valores, quer dizer que conseguimos encontrar o intervalo em que ela cresce, que é em e , e no resto da função ela decresce, que é em .
Passo 7
Para procurar os pontos mínimos, é importante olhar onde a função decresce, porque quando ela parar de decrescer e mudar o sinal, ali teremos nosso ponto.
Mas nesse caso, a função decresce de até , mas bem no momento em que ela para de decrescer temos uma assíntota, então não temos ponto de mínimo.
Há máximo local em porque a função está crescendo até e nesse momento ela começa a decrescer, formando aquela famosa montanhazinha /\.
Passo 8
Como é positiva para , em todo esse intervalo então sabemos que ela faz o sorrisão, e é côncava para cima, em , e côncava para baixo em que é o restante.
Lembra que a gente tem uma assíntota em
Então, nesse ponto a concavidade deveria mudar o sinal e nos dar um ponto de inflexão, mas por conta da assíntota, ele não existe.
Passo 3
Após esse mundaréu de passos, vamos para o gráfico!! Agora fica fácil de visualizar tudo, dá uma olhada naquela assíntota e uma relida nos passos para fixar tudo na cabeça!
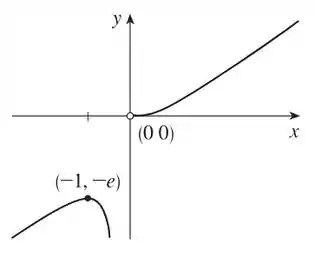
Resposta
Vide o passo a passo.