Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 4.6 - Ex. 22
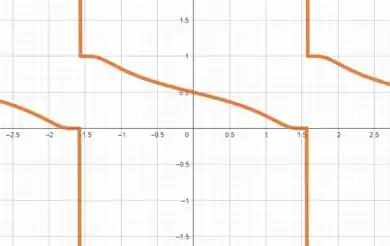
Use um sistema de computação algébrica para fazer o gráfico de e encontrar e . Utilize os gráficos dessas derivadas para estimar os intervalos de crescimento e decrescimento, valores extremos, intervalos de concavidade e pontos de inflexão de .
Passo 1
E aí! tudo certinho?
Nesse problema foi dada a função
E nosso objetivo é plotar os gráficos de e para encontrar os intervalos de crescimento e decrescimento, de concavidades, os valores extremos e os pontos de inflexão.
Tem ideia de como fazemos isso?
Bom... vamos começar calculando e usando um sistema de computação e plotar seus gráficos.
A partir do gráfico de podemos encontrar informações importantes... a inclinação de está diretamente relacionado a , então se , a inclinação de é positiva e se a inclinação de é negativa. Além disso, quando temos pontos críticos de e para analisar se são valores extremos, temos que verificar nesse ponto.
Já em podemos determinar os intervalos de concavidades... se a concavidade é para cima e se a concavidade é para baixo. E para determinar se os pontos críticos obtidos em são de máximos ou mínimos verificamos o sinal de ... se o ponto é de máximo, se o ponto é de mínimo e se temos um ponto de inflexão.
Sacou? Bora começar!
Passo 2
Vamos começar analisando ...
Usando uma ferramenta computacional e uma ferramenta gráfica, temos que
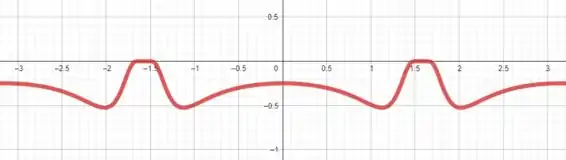
A partir desse gráfico podemos concluir que para todo a função possui inclinação negativa pois .
Podemos perceber tambem que possui dois candidatos a pontos extremos: e .
Tranquilo até aqui?
Passo 3
Agora vamos repetir o processo do início do passo 2 para obter
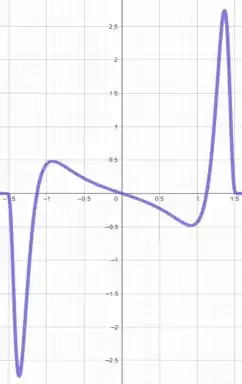
Aqui podemos observar que nos intervalos e a função possui concavidade voltada para cima pois e nos intervalos e a função possui concavidade voltada para baixo pois .
Agora vamos analisar os pontos críticos obtidos no passo anterior...
Em e a função é praticamente zero, então não possui pontos extremos, mas sim pontos de inflexão. Além desses pontos tambem é um ponto de inflexão pois .
Show?
Passo 4
Para confirmar tudo que encontramos até aqui, vamos plotar o gráfico de .
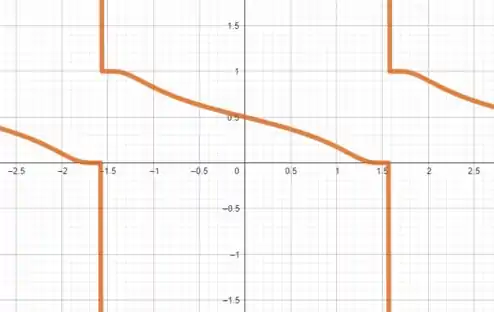
Aqui podemos perceber os intervalos de inclinação, as concavidades e os pontos de inflexão!
Perceba que a função é periódica e fizemos analise apenas em um intervalo, porém o que concluímos se repete a cada período.
E aí! o que achou? Responde Aí!
Resposta
