Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.6 - Ex. 28
Descreva a mudança no gráfico de à medida que varia. Faça o gráfico de vários membros da família para ilustrar as tendências que você descobriu. Em particular, você deve investigar como os pontos de máximo e mínimo e os pontos de inflexão movem-se quando varia. Você deve também identificar qualquer valor intermediário de no qual o aspecto básico da curva mude.
28.
Passo 1
Fala aí, pessoal. Tudo certinho?
Bom, essa questão dá pra gente a função
E pede pra gente fazer o gráfico de vários membros da família para ilustrar as tendências.
Devemos investigar como os pontos de máximo e mínimo e os pontos de inflexão movem-se quando varia.
E identificar qualquer valor intermediário de no qual o aspecto básico da curva mude.
Ou seja, queremos conhecer o comportamento da função de acordo com a variação do coeficiente .
Para isso, vamos traças as curvas e analisar suas características.
Vamos lá.
Passo 2
Vamos começar com valores negativos de .
Como , temos:
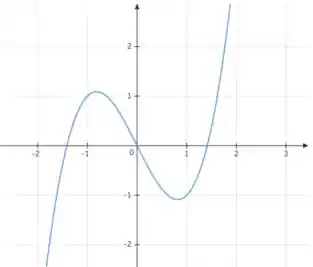
Temos valores de máximo e mínimo locais bem definidos.
Passo 3
Agora, vamos aumentar o valor de um pouco.
Para , temos:
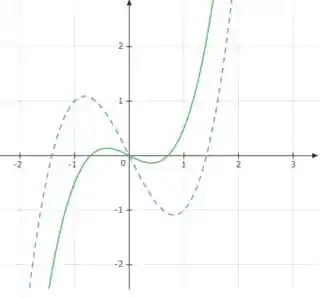
Observe que o gráfico sofreu uma modificação em seus pontos de máximo e mínimo locais.
Passo 4
Agora vamos usar valores positivos para
Fazendo , teremos:
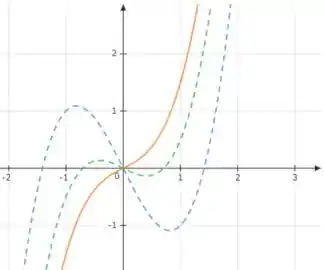
E vemos que a curva ficou mais suave.
Passo 5
Agora para , temos:
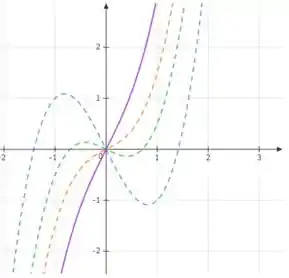
Ela suavizou ainda mais, perdendo seus valores de máximo e mínimo local.
Agora perceba que quanto maior o valor de , mais rapidamente a função varia.
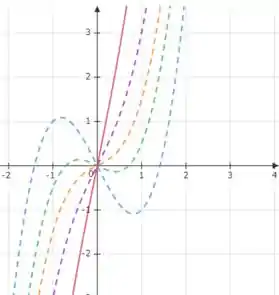
Resposta
No desenvolvimento.