Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 9.2 - Ex. 16
Use um sistema de computação algébrica para desenhar um campo de direções para a equação diferencial dada. Obtenha uma impressão e esboce uma curva solução que passe por . Use o SCA para desenhar a curva solução e compare o resultado com seu esboço.
Passo 1
Show de bola, galera....Pra resolver essa questão não tem mistério.
Vamos esboçar agora o campo de direções associado a este problema juntamente com a nossa possível solução que passa pelo ponto : 
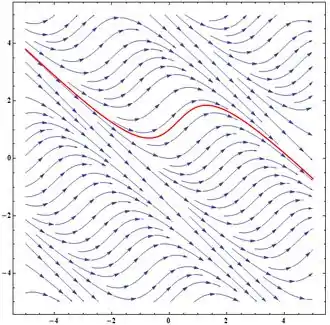
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Demonstrar que se uma função f ( t ) está no núcleo de D-a , então f ( t ) é dada por f ( t )=k e a t , onde k é um número real.Sugestão: Considere a função f t e - a t e mostre que ela é constante.
Aplicar os operadores lineares à função 𝑐os(w t) .
Provar que toda combinação linear (com coeficientes em IR) das funções s e nw t e c o sw t pertence ao núcleo de D 2 + w 2 .
Aplicar os operadores lineares à função 𝑐os(w t) .
Aplicar os operadores lineares à função 𝑐os(w t) .