Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.3 - Ex. 32
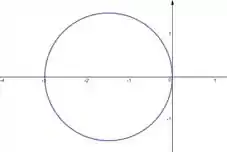
Esboce a curva com a equação dada.
Passo 1
Fala Guerreiro! Tranquilo? O que acha de iniciarmos esta questão entendendo o que a equação representa, e analisar seu comportamento para que assim podermos determinar seus pontos críticos e construir o gráfico?
Boa ideia? bora lá.
Passo 2
A equação descreve uma curva em coordenadas polares. Em que representa a distância radial a partir da origem e é o ângulo em relação ao eixo positivo (em radianos).
O termo determina a variação de conforme varia de a .
O que a equação representa?
Nessa questão, assim como na anterior, temos o em função de , para construirmos esse gráfico temos que calcular o valor de para diversos ângulos e estimar o gráfico, ou podemos mudar para coordenadas cartesianas.
Passo 3
Utilizando o segundo método novamente, sabemos que , se isolarmos o ficamos com
Substituindo na equação
Multiplicando dos dois lados
Outra relação importante é que , substituindo temos
Passo 4
Essa fórmula tem como cara uma circunferência deslocada, igual da ultima questão, para descobrirmos o raio e o centro, precisaremos completar quadrado.
Para isso vamos passar todos os termos para a esquerda e destacar com o que vamos trabalhar
Temos que transformar essa parte em algo da forma , isto é um quadrado de uma soma, um quadrado perfeito mais uma constante qualquer, portanto na igualdade
Abrindo o quadrado em parênteses
Passo 5
Analisando esta equação temos polinômios semelhantes.
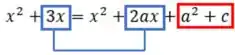
Pela igualdade de polinômios temos o seguinte sistema:
Substituindo o valor de , obtermos o valor de .
Passo 6
Substituindo os termos e encontrados.
Substituindo a equação acima na equação original do enunciado,
Passo 7
A partir da equação encontrada no Passo 3, podemos identificar o valor do raio e o ponro onde fica localizado o centro da circunferência.
centrada no ponto .
No plano:
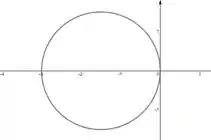
Resposta
