Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.6 - Ex. 38
Use o Teorema 5.6.8 para determinar qual dos símbolos ou deve ser inserido onde indicado.
(Teorema dado no livro)
Passo 1
O Teorema citado na questão diz que se temos duas função e integráveis no intervalo , se tivermos para todo no intervalo, teremos então . O que queremos é então provar que uma das funções dadas é sempre maior que a outra no intervalo , para então aplicar o teorema.
Passo 2
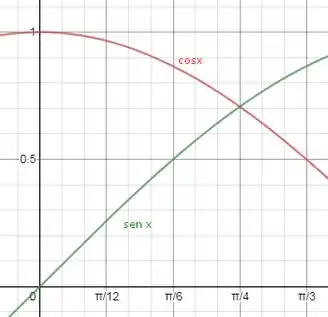
Se esboçarmos as funções seno e cosseno no intervalo , percebemos que o cosseno é maior que o seno em e ao longo do intervalo, e no final do intervalo temos . Podemos afirmar então que no intervalo, e então aplicando o teorema a primeira integral será maior ou igual à primeira.
Resposta
Exercícios de Livros Relacionados
Determine a norma da partição P = { - 2 ; - 1 . 6 ; - 0 . 5 ; 0 ; 0.8 ; 1 }
Faça o gráfico de f ( x ) no intervalo dado. Divida o intervalo em quatro subintervalos de comprimento igual. Em seguida, adicione os retângulos associados com a soma de Riemann ∑ k = 1 4 f ( c k ) Δ
Faça o gráfico de f ( x ) no intervalo dado. Divida o intervalo em quatro subintervalos de comprimento igual. Em seguida, adicione os retângulos associados com a soma de Riemann ∑ k = 1 4 f ( c k ) Δ
Determine a fórmula para a soma de Riemann obtida dividindo o intervalo [ a , b ] em n subintervalos iguais e usando a extremidade direita para cada c k . Depois, tome o limite dessas somas quando n →
Determine a fórmula para a soma de Riemann obtida dividindo o intervalo [ a , b ] em n subintervalos iguais e usando a extremidade direita para cada c k . Depois, tome o limite dessas somas quando n →