Para quais valores de o polinômio tem dois pontos de inflexão? E um ponto de inflexão? E nenhum? Ilustre, fazendo o gráfico de para vários valores de . Como o gráfico varia quando decresce?
Passo 1
Eaee, belezinha??? Bom... o enunciado nos dá a seguinte função:
Onde é uma constante.
Queremos encontrar os valores de para os quais a função tenha dois pontos de inflexão.
Mas o que são esses pontos??
Os pontos de inflexão são aqueles em que há troca de sinais da derivada.
Também queremos encontrar os valores de para um e nenhum ponto de inflexão.
Depois temos que plotar o gráfico de para diferentes valores de e analisar o seu decrescimento.
Passo 2
Vamos achar a segunda derivada de para achar os pontos de inflexão:
Fazendo a primeira derivada:
Fazendo a segunda derivada:
Passo 3
Vemos que o gráfico de é uma parábola, assim tem duas raízes, assim muda de sinal duas vezes, tendo dois pontos de inflexão.
E isso acontece quando o delta de é positivo, assim:
Temos agora que se:
Aqui temos que é em um ponto, mas não há ponto de inflexão, já que nunca muda de sinal.
E por último:
Aqui nunca troca de sinal, assim não há ponto de inflexão.
Passo 4
Aqui temos a ilustra��ão, fazendo o gráfico de para vários valores de :
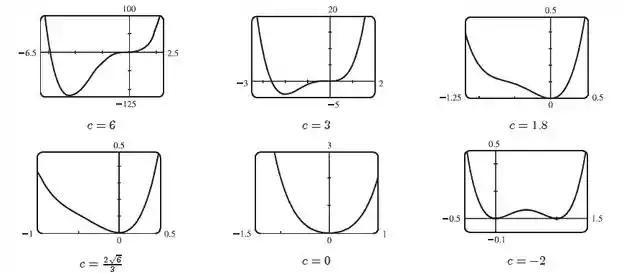
Passo 5
Para positivos muitos grandes de , o gráfico de tem dois pontos de inflexão e um grande mergulho a esquerda no eixo .
A medida que decresce, o gráfico de se torna mais plano para , e eventualmente o mergulho sobe acima do eixo e então desaparece totalmente, junto com os pontos de inflexão.
Enquanto continua a decrescer, os pontos de mergulho e os pontos d einfelxão reaparecem, a direita da origem.
Resposta
Dois pontos de inflexão para , nenhum valor de para um ponto, e e para nenhum ponto de inflexão.
A medida que decresce, o gráfico de se torna mais plano para , e eventualmente o mergulho sobe acima do eixo e então desaparece totalmente, junto com os pontos de inflexão. Enquanto continua a decrescer, os pontos de mergulho e os pontos d einfelxão reaparecem, a direita da origem.