Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.5 - Ex. 32
Prove que os gráficos das funções secante e cossecante não têm pontos de inflexão.
Passo 1
Para determinar os pontos de inflexão do gráfico, ou seja, o ponto onde a função muda a direção da concavidade, devemos obter a derivada segunda da nossa função. Para secante:
Uma vez descoberta a derivada segunda, os pontos de inflexão são caracterizados por . Então:
Sendo assim, o termo não poderá ser igual a 0. Analisando o gráfico:
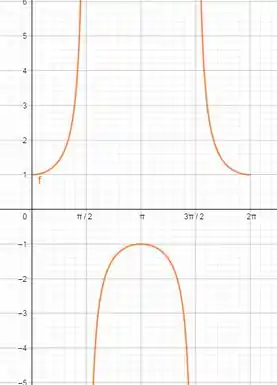
Sendo assim, não há pontos de inflexão para a função secante.
Passo 2
Analisando a função cossecante:
Uma vez descoberta a derivada segunda, os pontos de inflexão são caracterizados por . Então:
Sendo assim, o termo não poderá ser igual a 0. Analisando o gráfico:
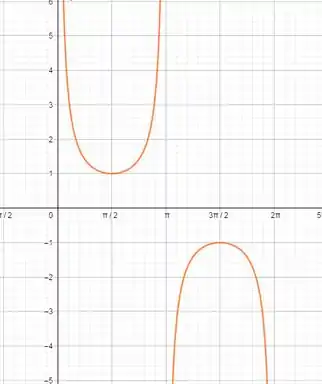
Sendo assim, não há pontos de inflexão para a função cossecante.
Resposta
Ei, a resposta está no passo a passo :)