Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.4 - Ex. 27
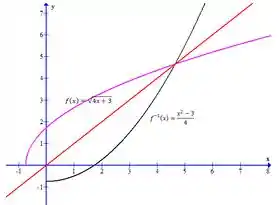
Encontre uma formula explicita para e use para traçar um gráfico e a linha na mesma tela. Para checar se está correto, veja se os gráficos de são refletidos pela linha.
Passo 1
Fala galera, tudo bem? O problema nos deu essa função
E pediu para encontrarmos uma fórmula explícita para a função inversa! Vamos relembrar como é esse processo?
Podemos dizer que e temos
Para achar a função inversa precisamos inverter: em vez de escrever em termos de , vamos escrever em função de ! Isso significa isolar do lado esquerdo e deixar todo resto do lado direito!
Uma característica legal da função inversa e da original é que se elas forem plotadas no mesmo plano cartesiano, elas serão simétricas em relação à reta
E é exatamente isso que o problema pede no final!
Mas relaxa, vou fazer passo a passo contigo!
Passo 2
Bom galera, primeiro vamos ver a função dada:
Temos que a restrição pra essa função é pois dentro da raiz deve ter um valor maior que zero!
E como a raiz tem coeficiente positivo
Beleza?
Agora vamos para a inversa! A ideia é isolar do lado esquerdo! Nossa função
Elevando ao quadrado dos dois lados
Isolando
Mudando a nomenclatura (onde era x é y e vice-versa):
As condições anteriores ainda valem, só lembrar de trocar x por y:
Passo 3
Agora traçamos o gráfico!
A função
A inversa
E ainda a reta
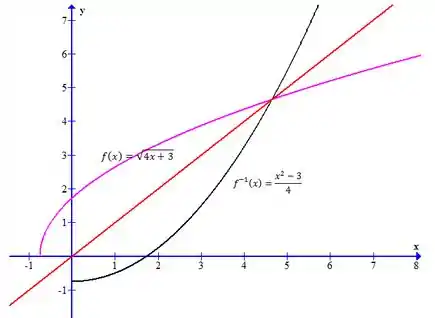
Note que em torno de as funções e são simétricas! Como havíamos previsto!
Beleza? É isso! Espero ter ajudado!
Resposta
