Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.4 - Ex. 4
Determine uma janela retangular apropriada para a função dada e use-a para fazer o gráfico da função.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente determinar uma janela retangular apropriada para plotar o gráfico da função:
Nesse tópico, estamos falando sobre calculadoras gráficas e computadores. Então, quando ele fala de escolher uma janela apropriada, significa escolher um intervalo na direção horizontal e na direção vertical que nos permita visualizar a nossa função da melhor forma, sem que a imagem esteja incompleta ou enganadora.
Pra isso, precisamos analisar a nossa função e verificar o intervalo que melhor a descreve. Conhecer o domínio e a imagem da função nos dá algumas pistas para escolher essa janela retangular. Só que nesse caso isso não ajuda muito, porque como se trata de uma função polinomial, ela vai estar definida para todo conjunto dos números reais.
Dessa forma, só nos resta fazer algumas tentativas usando a calculadora gráfica e levando em consideração que, por se tratar de uma equação do terceiro grau, ela terá raízes, então a curva vai encontrar o eixo três vezes.
Vamos lá!
Passo 2
Então, basicamente, devemos procurar uma janela que contenha todas as raízes da função nesse caso.
Se iniciarmos com a janela retangular por onde varia de a e também, teremos o gráfico abaixo:
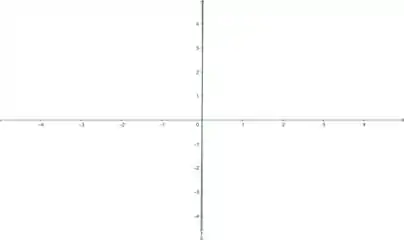
Parece que o gráfico (em verde) está tão próximo de ser vertical e chega se parece com o eixo .
Passo 3
Agora usando o recurso do zoom da calculadora gráfica para mudar a janela retângula para por , teremos o gráfico:
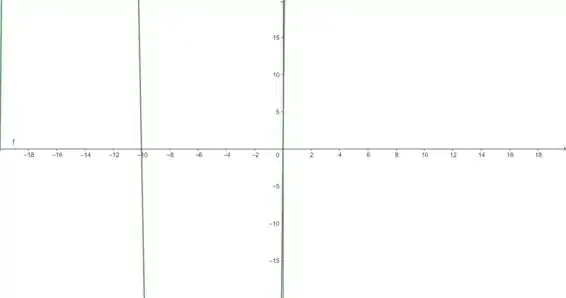
O gráfico parece ser formado por retas verticais, mas sabemos que isso não está correto, porque temos um polinômio de terceiro grau como função.
Passo 4
Olhando com mais cuidado, a gente percebe que precisa de mais espaço na direção vertical e na direção horizontal para ver os pontos onde a curva corta o eixo e onde ela tem seus picos e seus vales. Então, vamos mudar a janela retangular para por . Assim, vamos ter:
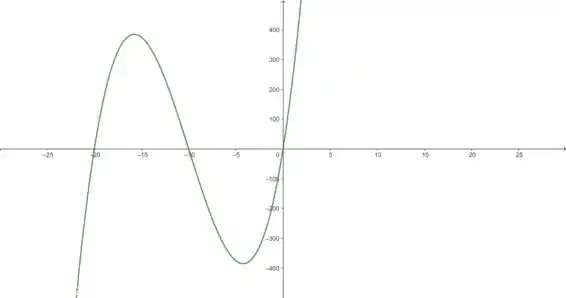
Agora sim isso tá com cara de curva de função polinomial, né? Percebe que agora dá pra ver certinho os pontos onde estão as raízes da função (quando ) e alguns pontos de máximo e mínimo da curva? Esses são os aspectos principais da função, nesse caso.
Isso significa que temos uma boa visualização da função e que essa é uma janela apropriada.
Valeu, galera! Até a próxima! 😉