Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 14.7 - Ex. 59

Você construirá uma caixa retangular aberta a partir de 12 pés2 de material. Quais dimensões resultarão em uma caixa de máximo volume?

Passo 1

Fala queridos, tudo bom com vocês? Prontos para detonar mais uma questãozinha? Bora! Seja a altura da caixa, a largura e o comprimento. Tirando quadrados de lado dos cantos do material, temos os seguinte diagrama:

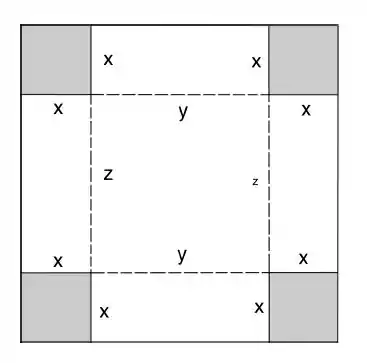
Dessa forma, podemos dizer que o comprimento da caixa é:

E a largura é:

Como temos um total de 12 pes, logo o comprimento vezes a altura é igual a 12 também. Logo:

Isolando :

Passo 2

Para encontrarmos a área máxima, temos que, a partir da derivada segunda da função que determina a área, encontrarmos o máximo local. Para:

Substituindo dentro dos pontos críticos:

, ,

Encontramos o local máximo para

Logo, a área máxima:

Resposta

Exercícios de Livros Relacionados

Determine os valores máximo e mínimo absolutos de f no conjunto D . f x , y = 2 x 3 + y 4 D = x , y | x ≥ 0 , y ≥ 0 , x 2 + y 2 ≤ 1

Nos Exercícios 31-38, encontre os máximos e mínimos absolutos das funções nos domínios dados. f x ,y = x 2 + y 2 na placa triangular fechada e limitada pelas retas x = 0 , y = 0 , y + 2 x = 2 no prime

Nos Exercícios 31-38, encontre os máximos e mínimos absolutos das funções nos domínios dados. T x ,y = x 2 + x y + y 2 - 6 x na placa retangular 0 ≤ x ≤ 5 , - 3 ≤ y ≤ 3 .

Nos Exercícios 31-38, encontre os máximos e mínimos absolutos das funções nos domínios dados. T x ,y = x 2 + x y + y 2 - 6 x + 2 na placa retangular 0 ≤ x ≤ 5 , - 3 ≤ y ≤ 0 .