Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.Questões para guiar sua revisão - Ex. 13
Como você determina a área da região , no plano de coordenadas polares? Dê exemplos.
Passo 1
Salve, fera! Tudo bem? Essa questão pode não ser tão simples. Vamos encará-la juntos?
Para calcular a área usamos a seguinte fórmula:
Por exemplo, para o anel com raio interno e raio externo , conforme a figura abaixo, temos a seguinte área:
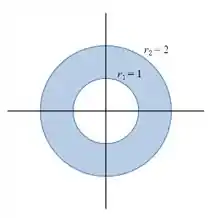
Espero ter ajudado! Abraços e até a próxima!
Resposta
Veja a explicação acima.
Exercícios de Livros Relacionados
Nos Exercícios de 1 a 36, faça um esboço do gráfico da equação dada 26. r = e θ / 3e s p i r a ll o g a r í t m i c a í
Nos Exercícios de 1 a 36, faça um esboço do gráfico da equação dada 25. r = e θ( e s p i r a ll o g a r í t m i c a ) í
Nos Exercícios de 1 a 36, faça um esboço do gráfico da equação dada 27. r = 1 θ( e s p i r a lr e c í p r o c a ) í
Esboce a região no plano que consiste em pontos cujas coordenadas polares satisfazem as condições dadas. 1 ≤ r ≤ 3 , π / 6 ≤ θ ≤ 5 π 6
Encontre uma equação polar para a curva representada pela equação cartesiana dada. y = 1 + 3 x