Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.1 - Ex. 45
Se você possui uma ferramenta que esboça gráficos de equações paramétricas, desenhe os gráficos das equações sobre os intervalos determinados nos Exercícios 41-48
45. Deltoide .
O que acontece se você substituir 3 por -3 nas equações para x e y? Desenhe os gráficos das novas equações e descubra.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Temos o seguinte gráfico para este caso, em que a equação paramétrica é fornecida no enunciado, sendo igual a
E com intervalo . Com isso, nós temos que
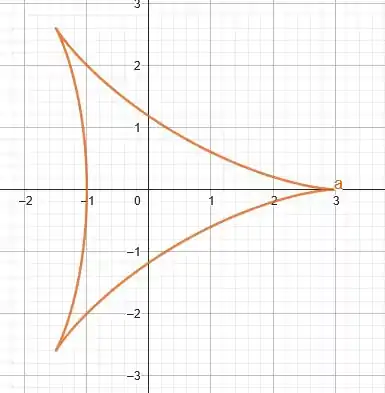
Passo 2
Quando mudamos de para , nós temos que
Relembrando que e , com isso,
Portanto, temos o seguinte gráfico
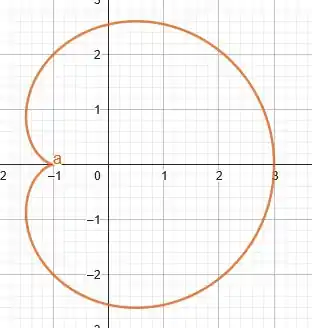
Resposta
Respondido acima!!!
Exercícios de Livros Relacionados
(a) Elimine o parâmetro para encontrar uma equação cartesiana da curva. (b) Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta. x = tan 2 θ ,y = sec
Nos exercícios 18 a 23, encontre uma equação da superfície de revolução gerada pela rotação da curva plana dada em torno do eixo indicado. Faca um esboço da superfície 18. x 2 = 4 y No plano XY, em to
Nos exercícios 18 a 23, encontre uma equação da superfície de revolução gerada pela rotação da curva plana dada em torno do eixo indicado. Faca um esboço da superfície 19. z = 4 + y 2 No plano ZY, em
Nos exercícios 18 a 23, encontre uma equação da superfície de revolução gerada pela rotação da curva plana dada em torno do eixo indicado. Faca um esboço da superfície 20. x 2 + z 2 = 16 No plano ZX,
Nos exercícios 18 a 23, encontre uma equação da superfície de revolução gerada pela rotação da curva plana dada em torno do eixo indicado. Faca um esboço da superfície 21. z = e - x 2 No plano ZX, em