Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.1 - Ex. 18
(a) Elimine o parâmetro para encontrar uma equação cartesiana da curva.
(b) Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta.
Passo 1
Okay, vamos lá resolver isso aí juntos!
O enunciado nos disse que, no intervalo , temos:
E
Queremos eliminar o parâmetro para encontrarmos uma equação cartesiana do tipo .
Para isso, vamos usar uma relação trigonométrica para criarmos nossa equação cartesiana, olha só:
Em seguida, devemos esboçar a curva da função que a gente encontrar e indicar com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta.
Agora bora lá!! 😉
Passo 2
Lembrando que o enunciado nos disse que e .
Da relação trigonométrica apresentada no passo 1, temos:
Assim, substituindo as variáveis do enunciado na relação, obtemos:
Isolando :
Passo 3
Cara, vamos lá pra parte do gráfico agora.
Vamos analisar o intervalo que nos foi dado. Vamos quebrar ele em duas partes:
Veja bem, quando , teremos que ambos tenderão para o infinito positivo.
Já para o outro extremo, também tendem pro infinito positivo.
Mas observe, quando , teremos que irá tender a zero e irá tender a , se observarmos os gráficos de e fica fácil essa visualização.
Assim, podemos dizer que:
Daí, nosso domínio do plano cartesiano será .
Passo 4
Assim, plotando o gráfico de e aplicando o que vimos no passo 3, temos:
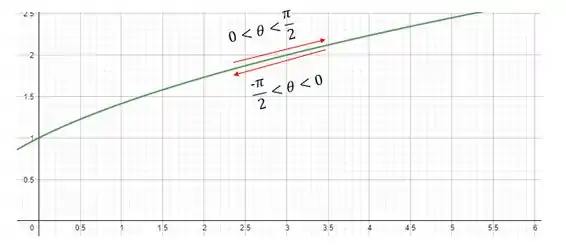
Quando temos o parâmetro indo de , vamos ter a saindo do infinito positivo para e , respectivamente, ou seja, decrescendo.
Já quando temos o parâmetro indo de , teremos saindo de e , e indo novamente para o infinito positivo, ou seja, crescendo.
Resposta
