Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.5 - Ex. 33
Se você traçar o gráfico da função
verá que parece ser uma função ímpar. Demonstre isso.
Passo 1
O problema fornece uma função dada por
Fazendo um esboço do gráfico dessa função, vemos que de fato ela parece ser uma função ímpar, já que ela é simétrica com relação a origem:
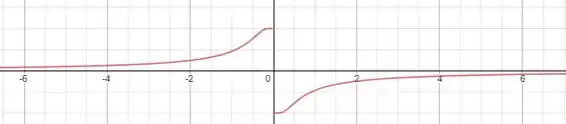
Passo 2
Agora vamos provar que a função é da fato ímpar. Para isso, temos que verificar que . Assim,
Multiplicamos o numerador e o denominador por :
Portanto,
Provamos assim que a função é ímpar!
Resposta
Demonstração e gráfico.
Exercícios de Livros Relacionados
Resolva em x sem usar uma calculadora. Use o logaritmo natural sempre que for necessário usar um logaritmo.
Resolva em x sem usar uma calculadora. Use o logaritmo natural sempre que for necessário usar um logaritmo.
Resolva em x sem usar uma calculadora. Use o logaritmo natural sempre que for necessário usar um logaritmo.
Simplifique a expressão sem usar uma calculadora:
Simplifique a expressão sem usar uma calculadora: