Racionalização

Fala aí, nós somos o Responde Aí, e nossa missão é ajudar você a mandar bem na sua prova.

Quando o assunto é fração a gente já fica até desanimado né? Oh bichinha pra tirar a paz de qualquer estudante kkkk. Agora imagina se aparece uma fração assim:

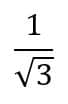
Essa raiz no denominador dificulta os cálculos e o que a gente quer é tirar ela dali de qualquer maneira e, para isso vamos usar o que chamamos de RACIONALIZAÇÃO.

Para obtermos uma fração equivalente, mas sem raízes no denominador nós vamos multiplicar o numerador e o denominador por uma coisinha chamada fator racionalizante. Beleza, mas que fator é esse? É sempre o mesmo? Como saber?

Relaxa, temos três casos particular:

• 1° CASO: Denominador com uma raiz quadrada

Nesse caso, o fator racionalizante vai sem sempre a própria raiz.

Vê esse exemplo aqui:



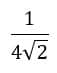
Temos uma única raiz no denominador, então vamos multiplicar o numerador e o denominador por essa mesma raiz:



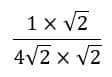
Agora só resolver que teremos uma fração equivalente e sem a raiz no denominador:



• 2° CASO: Denominador com uma raiz, com índice diferente de 2

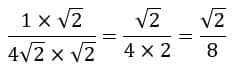
Nesse caso o denominador vai ter essa carinha aqui:



E o fator racionalizante vai ser:



Esse assusta uma pouquinho né? Mas não é esse bicho de sete cabeças não. Vem aqui comigo fazer um exemplo:



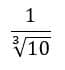
O denominador tem uma raiz e não é quadrada, é cúbica. Olha bem pra essa raiz e nota que $a=10$, $n=3$ e $m=1$. Então nosso fator racionalizante será:



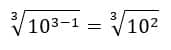
Sacou? Agora só temos que multiplicar:



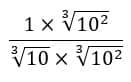
Como as raízes não são quadráticas, é um pouquinho mais chatinho de resolver, temos que colocar as raízes em forma de potência:



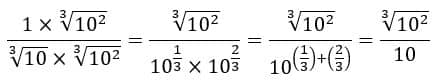
E prontinho!

• 3° CASO: Denominador com uma soma ou subtração, onde pelo menos um dos termos é uma raiz

Nesse caso, o fator racionalizante será a mesma soma ou subtração que temos no denominador, só vai trocar o sinal, assim:

Vamos lá pro nosso exemplo:

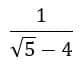
Temos uma subtração no denominador e pelo menos um termo é uma raiz, então o nosso fator racionalizante será essa mesma expressão, mas com o sinal trocado:

Agora, só temos que multiplicar e resolver:

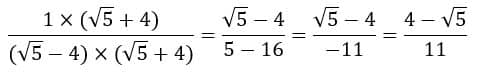
Finalizamos. Agora quando se deparar com um exercício, basta ver em que caso se encaixa e mandar ver =)