Fórmula de Bhaskara

A fórmula de Bhaskara serve para resolvermos equações do segundo grau. Ela tem essa carinha aqui:

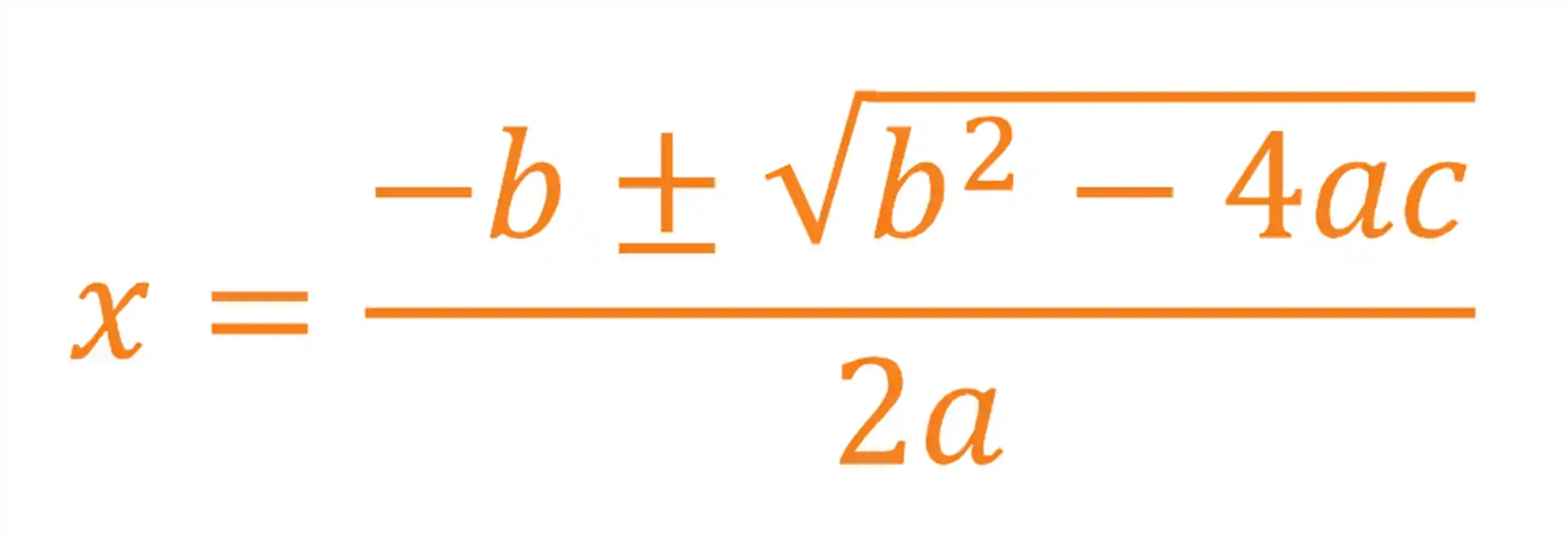
Onde:

• é um ou dois valores, dependendo do valor de Delta, lembrando que Delta, também chamado de Discriminante, é o que determina para gente se a equação vai ter duas raízes reais, duas raízes reais iguais ou duas raízes imaginárias.
• e são os coeficientes da equação de segundo grau:

Exemplo: Uma bola lançada a partir de um canhão descreve uma trajetória parabólica de acordo com a equação . Descubra a posição do canhão no momento do lançamento e a posição em que a bala toca o solo.

Para resolver a questão vamos utilizar a fórmula de Bhaskara e esperamos encontrar duas raízes a primeira nos dirá a posição inicial do canhão e a segunda o ponto em que a bola atinge o solo. Então:

Substituindo os dados e calculando:

A nossa primeira raiz é igual a:

A segunda raiz:

Logo o canhão está posicionado em e o lançamento da sua bola atinge .

Prontinho! Agora você pode dar uma conferida no nosso conteúdo sobre Matemática Básica! Aqui no Responde Aí temos conteúdo em texto, vídeo, exercícios resolvidos passo a passo e mais!

Você também pode clicar aqui pra conferir a resolução de milhares de questões de livro! 🤩🤩🤩