Grandezas Diretamente e Inversamente Proporcionais
Produzido por Marcelo LuizTeoria
Introdução
Já parou pra pensar sobre a proporcionalidade das coisas em nosso dia a dia?? As proporções, de maneira direta ou indireta, estão presentes na maioria das coisas que fazemos.
Dê uma olhada nesses dois exemplos:
1º Quanto mais você estuda no Responde Aí, mais fácil fica de tirar aquele notão!!!

Perceba que nesse caso, quanto mais você faz algo (estudar no Responde Aí), mais aumentam suas chances em algo (mandar bem na prova).
Em casos como esse, as grandezas dependem uma das outras e a taxa de crescimento de uma está diretamente ligada com a taxa de crescimento da outra. Podemos ver essas relações no dia a dia em diversas ocasiões:
- Quanto mais carros nas ruas, mais trânsito.
- Quanto mais pessoas no banco, mais fila.
- Quanto mais exercícios físicos eu faço, mais saudável eu fico.
Todas essas relações de crescimentos entre grandezas são chamadas de DIRETAMENTE PROPORCIONAIS.
2º Quanto mais passam os dias do mês, menos dinheiro eu tenho na minha conta.

Aqui, quanto mais acontece algo (passar os dias do mês), menos temos de algo (dinheiro na conta).
Nesses casos, as grandezas também dependem uma das outras assim como no anterior, porém, a diferença aqui é que o aumento da taxa de crescimento de uma das grandezas faz com que haja uma taxa de decrescimento na outra. Podemos ver casos como esses em:
- Quanto mais rápido você vai, menos tempo demora.
- Quanto mais pessoas na festa, menos bebida terá para cada uma.
Essas relações entre as grandezas são chamadas de INVERSAMENTE PROPORCIONAIS.
Como definir Grandezas?
Beleza, mas o que são grandezas?
Para nossos cálculos, vamos considerar que grandeza é tudo aquilo que pode ser medido. E por que isso é importante?
Pense no seguinte problema:
Um homem vai ao açougue e pretende gastar reais em carne para fazer um churrasco no fim de semana. Sabendo que quilo de carne que custa reais, quantos gramas ele conseguirá comprar com reais?
De início já podemos perceber que se trata de grandezas diretamente proporcionais, pois quanto mais dinheiro o homem tem, mais carne ele poderá comprar. Fazendo uma continha simples temos que:
Ou seja, o homem tem vezes mais dinheiro que o necessário para comprar , logo, ele também pode comprar vezes mais carne. Então, com seus reais ele poderá comprar de carne.
Já descobrimos que agora ele pode comprar de carne, mas o enunciado pergunta quantos gramas ele poderia comprar. O que fazer??

Relembrando...
Bom, para isso precisamos relembrar como converter unidades de medidas, que nada mais é que transformar uma medida como a grama para quilograma , centigrama , etc. E para isso, lá vai um macete pra salvar sua vida:
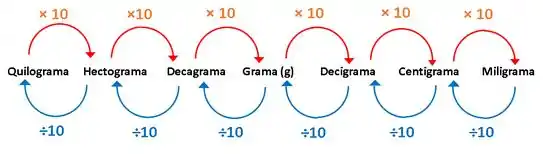
Mas isso serve apenas para as gramas?
Não!! Você pode usar isso em muitos outros tipos de grandezas e obter algo do tipo:
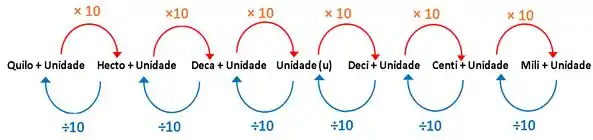
Perceba que a Unidade não está declarada, isso quer dizer que essa unidade pode ser de diferentes tipos: Metro, grama, litro...
MUUUUUUUITO IMPORTANTE!!! Essas regras não valem para todos os tipos de medidas. Algumas grandezas (normalmente associadas com o tempo) tem regras únicas e, portanto, não se aplicam tais transformações. Entre essas grandezas estão:
- Temperatura.
- Meses, semanas, dias.
- Décadas, séculos, milênios.
Agora já temos todas as ferramentas necessárias, bora terminar o exercício...
Já tinhamos achado anteriormente que a quantidade de carne que o homem conseguiria compra com reais era . Agora é só colocar em prática o que vimos nas tabelas:
Logo:
E tá resolvido, com reais o homem conseguirá comprar gramas de carne.
E aí, que tal agora fazer alguns exercícios de fixação para ficar craque!?