Introdução aos Triângulos
Produzido por Marcelo LuizTeoria
Introdução
Os triângulos são um dos assuntos mais importantes dentro da trigonometria, através do estudo deles conseguimos extrair muitas propriedades que serão extremamente úteis em cálculos mais complexos.
Tá, mas o que seriam os triângulos?
O triângulo é um polígono que possui três lados e três ângulos.

Esses ângulos vão ser muito importantes quando quisermos classificar os triângulos em grupos diferentes, mas antes, vamos ver algumas propriedades que são comuns a todos os triângulos.
Propriedades do Triângulos
Os triângulos são compostos por vértices, lados e ângulos.
A soma dos ângulos internos dos triângulos resulta em .
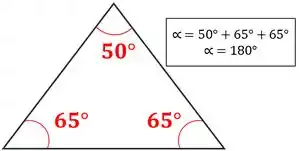
A soma dos ângulos externos dos triângulos resulta em .

Mas por que os ângulos são tão importantes quando trabalhamos com os triângulos?
Os ângulos determinam qual será o tipo do triângulo, ou seja, dependo da disposição dos seus ângulos, o triângulo pode pertencer à classes diferentes,
Tipos de Triângulos
Triângulo Equilátero
No triângulo equilátero, todos os seus lados tem a mesma medida e por consequência, todos seus ângulos também.
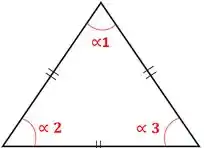
Triângulo Isósceles
O triângulo isósceles tem dois de seus lados iguais, dessa forma, dois de seus ângulos também são equivalentes.
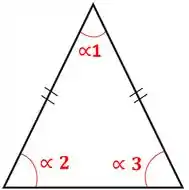
Triângulo Obtuso
Um de seus ângulos é maior que .

Obs: O triângulo obtuso também pode ser considerado isósceles caso .
Triângulo Escaleno
Nenhum de seus lados são iguais.
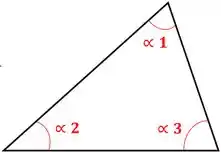
Triângulo Retângulo
Um de seus ângulos é de , é um dos mais importantes para trigonometria.
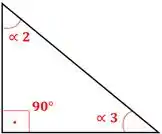
Obs: O triângulo retângulo também pode ser considerado como isósceles caso .
Mediana e Baricentro
O baricentro de um triângulo também é conhecido como seu centro de gravidade, centro de massa ou ponto de equilíbrio.
Mas como baricentro e medianas se relacionam?
A mediana é o ponto médio de um lado que se liga com o vértice oposto ao lado:
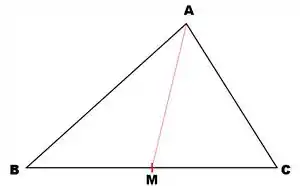
é o ponto médio entre .
Podemos fazer isso com os outros dois lados e teremos algo assim:
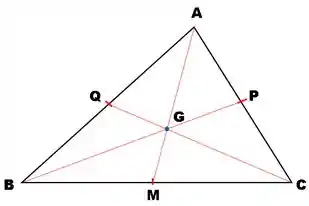
Os pontos , e são pontos médios dos lados.
Quando ligamos os pontos das medianas com os vértices opostos observamos que as três medianas se cruzam em um único ponto.
Esse ponto (Ponto ) será o baricentro do triângulo.
E aí, já está craque com os triângulos? Bora praticar...