Exercícios de Semelhança de Triângulos - Lista de Exercícios Resolvida

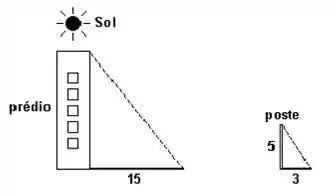
A sombra de um prédio, em um terreno plano, em uma determinada hora do dia, mede 15 m. Nesse mesmo instante, próximo ao prédio, a sombra de um poste de altura 5 m mede 3 m. A altura do prédio, em metros, é:

Sabendo que os triângulos abaixo são semelhantes, determine:

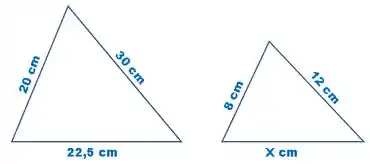
a) O valor de .

b) A razão entre os triângulos.

A ilustração a seguir representa uma mesa de sinuca retangular, de largura e comprimento iguais a 1,5 e 2,0 m, respectivamente. Um jogador deve lançar a bola branca do ponto e acertar a preta no ponto , sem acertar em nenhuma outra, antes. Como a amarela está no ponto A, esse jogador lançará a bola branca até o ponto , de modo que a mesma possa rebater e colidir com a preta.

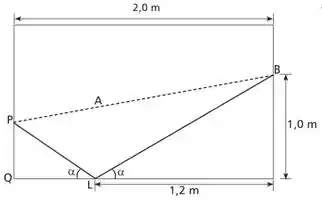
Se o ângulo da trajetória de incidência da bola na lateral da mesa e o ângulo de rebatimento são iguais, como mostra a figura, então a distância de a , em , é aproximadamente:

a) 67

b) 70

c) 74

d) 81

Um triângulo tem seus lados dados por:

• Lado 1 ;
• Lado 2 ;
• Lado 3 .

Qual será a medida dos lados de um triângulo cuja razão é vezes maior que o primeiro triângulo?

Existem alguns procedimentos que podem ser usados para descobrir se dois triângulos são semelhantes sem ter de analisar a proporcionalidade de todos os lados e, ao mesmo tempo, as medidas de todos os ângulos desses triângulos. A respeito desses casos, determine quais alternativas estão incorretas e quais estão corretas:

a) Para que dois triângulos sejam semelhantes, basta que eles tenham três ângulos correspondentes congruentes.

b) Para que dois triângulos sejam semelhantes, basta que eles tenham dois lados proporcionais e um ângulo congruente, em qualquer ordem.

c) Dois triângulos que possuem apenas dois ângulos correspondentes congruentes não podem ser considerados semelhantes.

d) Para que dois triângulos sejam congruentes, basta que eles tenham os três lados correspondentes com medidas proporcionais.

Dado dois triângulos semelhantes, sabendo que a razão de semelhança é igual a e que as medidas dos lados do triângulo maior são iguais a , e , qual é o perímetro do triângulo menor?

Estudando os triângulos determine o valor de , sabendo que os lados e são paralelos.

Qual caso garante a semelhança entre os triângulos abaixo?

Uma pessoa com de altura deseja encontrar a altura de um edifício. Ela mediu o comprimento de sua sombra e da sombra do edifício ao mesmo tempo e obteve e , respectivamente. Qual é a altura do prédio?