Fundamentos de Lógica e Linguagem Matemática
Produzido por Erick PinhoTeoria
Implicação
Cara, para tudooooooo! Esse conectivo, representado por , é o mais importante! Acho que você já tá cansado de ver:
Em que lemos “ implica ”.
É aquele que expressa uma relação de implicação, mas não de causa-efeito, ela apenas estabelece uma relação entre os valores lógicos da implicação e os valores lógicos de e .
Nessa relação, é chamada hipótese ou premissa e é a tese ou conclusão.
Olha um exemplo bem doido:
Se adotarmos:
Nossa proposição é:
Essa implicação é verdadeira, pois é verdadeira e também. Mas perceba que não tem nada a ver uma coisa com a outra. Apenas julgamos a setinha, baseado na hipótese e na tese.
Olha esse que doideira:
Cara, pasme se quiser, isso é verdadeiro!!! Sabe por que?
A hipótese é falsa e a tese também é, então a implicação é verdadeira. Saca só a tabela verdade:
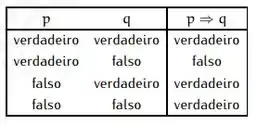
A única forma da implicação ser falsa é se a hipótese for verdadeira e a tese for falsa.
E como fica a negação disso?
Recíproca, contrapositiva, inversa e relação de equivalência
Vamos conhecer as primas da implicação. Dada uma implicação do tipo:
E já te adianto o seguinte: a implicação é equivalente à contrapositiva. Como eu sei disso? Você sempre pode dizer que duas proposições compostas são equivalentes se elas possuem a mesma tabela verdade. Olha a tabelinha:
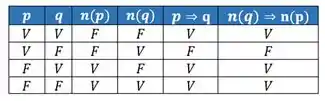
Percebe que os valores verdades das duas últimas colunas são iguais, então são equivalentes.
Olha tabela das três proposições que vimos agora:
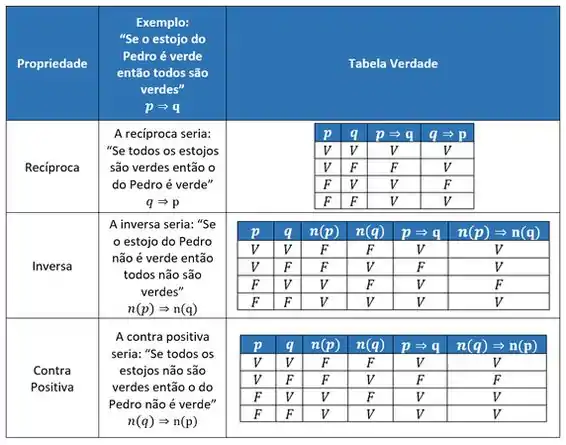
Perceba que a recíproca e a inversa são equivalentes, pois suas tabelas verdade são iguais (olhe a última coluna)!
Finalmente, o conectivo
É chamado de bicondicional ou biimplicação. A gente lê isso como “p se e somente se q”.
Para dizer que isso é verdade ou não, basta que seja verdade.
Exemplo:
Vamos ver se a implicação é verdadeira:
Isso não é verdade, pois é irracional e é racional. Nem precisamos fazer a recíproca, já temos aqui que a biimplicação é falsa.
Dizemos que é condição suficiente para se é verdadeira e dizemos que é condição necessária para se é verdadeira. No caso de biimplicação, ou seja, a implicação e a recíproca são verdadeiras, dizemos que é uma condição necessária e suficiente para .
Deixo aqui a tabelinha da negação pra você de todos os conectivos e quantificadores que vimos até agora:
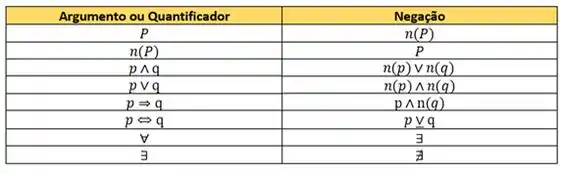
Múltiplos Quantificadores
Bom, já vimos os quantificadores e , mas ainda não os vimos juntos! Simmmm, chegou a hora de juntar esse dois e ver a bagunça que fica hahaha
Já vou te avisando, porque sou sua amiga, que A ORDEM IMPORTA. Então toda vez que você se depara com algo assim:
Já repara em quem tá aparecendo primeiro! Vamos traduzir isso aí pro português: “Para todo número real , existe um número real tal que ”.
Cara, isso é verdade. Qualquer número que você pegue , se você elevá-lo ao quadrado, também será um número real, que chamaremos de .
Agora vamos inverter essa brincadeira:
Agora traduzindo para o português: “Existe um número real tal que para todo número real , ”. Isso não é verdade, cara. Tipo, escolhe um número real , pode ser o ou qualquer outro da sua preferência. Me diga, é verdade que PARA TODO E QUALQUER real, ???
Não é verdade, você pode pegar o . E isso deu errado não foi porque escolhemos o , mas porque não vai funcionar com nenhum número.
Agora vamos aprender a negar essas estruturas. Lembre-se: onde é “tal que” vira vírgula e onde é vírgula vira “tal que”.
Troquei o por e vice-versa! Legal né? Partiu exercícios!!!