Conectivos lógicos
Produzido por Erick PinhoTeoria
Fala aí, aqui é o Responde Aí, e vamos falar sobre os princípios da lógica!
A matemática possui uma linguagem e símbolos próprios, assim como nós temos o português e o nosso alfabeto. Então dá uma olhada nessa tabela com os principais conectivos lógicos:
Mas não precisa se desesperar, porque aqui nós vamos fazer de tudo para você compreender um pouco sobre os conectivos lógicos. Mas antes de mais nada, você precisa começar entendendo o que é uma preposição.

Preposições
Uma das coisas mais importantes nessa lógica matemática são as proposições. As proposições nada mais são que frases afirmativas às quais são atribuídos valores de VERDADEIRO ou FALSO.
Olha essas duas frases aqui:
- Eu sou uma pessoa
Essas frases são proposições, porque podemos dizer se elas são falsas ou verdadeiras.
Agora olha essas outras duas aqui:
- Está quente hoje;
- Hoje vai chover?
Podemos dizer que essas frases são verdadeiras ou falsas? Não, porque estar quente ou não é bem relativo e não existe dizer que uma pergunta é falsa ou verdadeira, portanto essas frases NÃO são proposições.
Entendendo os conectivos lógicos
Agora que já sabemos o que são proposições podemos falar sobre os elementos de lógica, ou seja, alguns os símbolos e conectivos lógicos que usamos na linguagem matemática para combinar proposições:
Vamos ver alguns exemplos da aplicação de alguns desses símbolos:
Condução
Uma conjunção é verdadeira se, e somente se, ambas as proposições forem verdadeiras.
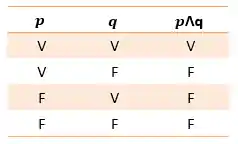
EXEMPLO:
Como:
Disjunção
A disjunção será falsa somente se ambas as proposições forem falsas.
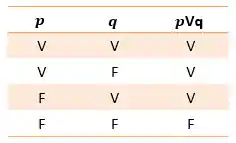
EXEMPLO:
Como:
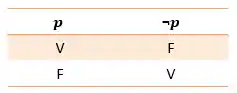
Negação
Quando negamos uma preposição estamos dizendo que ela não é verdadeira. Desse modo, se a proposição
Combinando os conectivos lógicos
Esses três são os elementos mais importantes.
Mas, se eu quiser combinar esses símbolos, ou seja, se eu quiser negar uma conjunção ou negar uma disjunção, o que acontece?
É bem tranquilo, toda vez que você negar um conjunção ou uma disjunção, lembra que uma vira a outra.
Se eu quero negar
Do mesmo modo, se eu quero negar
Show de bola?
Vídeo
Nós temos esse conteúdo em vídeo também, é só conferir aqui em baixo 👇🏾: