Inequações exponenciais e logarítmicas
Produzido por Erick PinhoTeoria
Inequações exponenciais com mesma base
Vimos na parte de funções exponenciais que uma função exponencial é sempre decrescente ou sempre crescente. Essa condição dependerá de sua base.
Se tivermos:
A função será decrescente, ao passo que:
Implicará na função sempre crescente.
Dessa maneira, por exemplo, a inequação:
Só será verdadeira se:
Com sinal trocado em relação a inequação correspondente, pois a base é menor que um e, portanto, a função é decrescente. Já:
Só será verdade se:
Com o mesmo sinal da inequação correspondente, pois a base é maior que e, portanto, a função é crescente.
Dessa forma, a inequação:
Implica na inequação:
Pois:
E a inequação:
Implica em:
Pois:
Essas inequações são simples de resolver, caso tenha dificuldade, volte as inequações de primeiro grau e depois você vai concordar comigo.
Inequações exponenciais de bases diferentes
Quando a base da inequação é diferente, como quando:
Precisamos dar uma manipulada nas bases para tentar igualá-las. Lembre que:
Substituindo essa beleza:
Agora ficou fácil:
Que sabemos resolver:
Inequações logarítmicas
Para inequações logarítmicas, temos a mesma ideia das exponenciais. Para a notação:
Se:
O sinal da desigualdade irá trocar, ou seja, para:
Temos a inequação correspondente:
Já para quando:
O sinal da desigualdade se mantém:
Sabendo que, quando a base está oculta na notação, ela é .
Tudo certo? Vamos aos exercícios.
Inequações exponenciais de bases diferentes
Inequações logarítmicas
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Determine o conjunto solução das seguintes inequações
a)
b)
c)
Passo 1
(a)
Como a base é maior que , a expressão é sempre crescente e como consequência:
Sim, é só isso.
Passo 2
(b)
Como a base tem valor entre e , a expressão é sempre decrescente, logo:
Passo 3
(c)
Aqui é um pouco mais complicado, mas nada demais. Vamos olhar as duas últimas condições:
Isso significa que, ou está entre e ou é maior do que . Vamos ver esses dois casos.
Para , a expressão é sempre decrescente, e invertemos a desigualdade:
Isolando:
Ops, mas nessa definimos que e obtemos , logo, para essa região, não há solução.
Passo 4
Agora, para , não invertemos a desigualdade e teremos:
Isolando:
Definimos e obtemos , então a solução será:
Resposta
(a)
(b)
(c)
Exercício Resolvido #2
Elaboração Própria
Determine o conjunto solução das inequações abaixo:
a)
b)
Passo 1
(a)
Temos que:
Pois qualquer número elevado dá .
Assim temos que:
Como as bases são menores que um e maiores que zero, cortamos o log e invertemos a desigualdade:
Passo 2
Agora muita atenção, detalhe importantíssimo: os argumentos dos logaritmos têm que ser positivos!! Log de zero, ou log de número negativo não pode!
E lá no enunciado a gente tinha o termo
Ou seja, também devemos ter:
Daí concluímos que:
Passo 3
Dito isso, vamos continuar!
Temos que:
Então:
Como a base é maior que um, cortamos o log e mantemos a desigualdade:
Passo 4
Vamos resolver as duas inequações separadamente:
Começando pela primeira:
Agora vamos pra segunda:
Juntando tudo, obtemos a solução final da inequação:
Passo 5
(b)
Antes de mais nada, vamos relembrar: os termos dentro dos logs têm que ser positivos, então, pra começo de conversa já sabemos que:
Beleza, agora podemos continuar. :)
Passo 6
Usando a propriedade do log:
Como:
Substituindo:
Como a base é maior que , cortamos o log e mantemos a desigualdade:
Distribuindo:
Agora é resolver inequação de segundo grau, que terá solução:
Mas vimos antes que , então a solução é:
Resposta
(a)
(b)
Exercício Resolvido #3
Elaboração Própria
Determine o conjunto solução da seguinte inequação:
Passo 1
A primeira coisa que vamos fazer, é colocar esses caras na mesma base.
Daí vamos escrever:
Passo 2
Como a nossa base é maior do que 1, podemos escrever:
Daí, teremos:
Temos aí um quociente entre uma equação do 2º grau e uma do 1º grau
Passo 3
As raízes de serão . E essa função é crescente.
A raiz de será igual a 0.Essa função do primeiro grau também será crescente.
Agora, vamos construir a nossa tabelinha
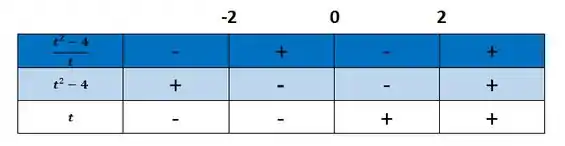
Vale observar que não podemos colocar o , pois isso geraria uma divisão por zero, uma indeterminação matemática.
Sendo assim, nosso conjunto solução será:
Resposta
Exercício Resolvido #4
Elaboração Própria
Determine o conjunto solução da seguinte inequação:
Passo 1
Vamos observar algumas coisas.
Primeiro: Essa função nunca será igual a zero, pois o numerador nunca será igual a zero.
Segundo: Se você prestar atenção, o numerador sempre será positivo, então para essa função ser negativa, o denominador precisa ser negativo.
Ou seja, podemos dizer:
Passo 2
Vamos resolver essa nova inequação agora
Como a base é maior do que 1, podemos escrever:
A raiz de vai ser igual a 0 e a raiz de vai ser igual a 1. As duas são funções do 1º grau CRESCENTES.
Sendo assim, vamos montar a nossa tabelinha.
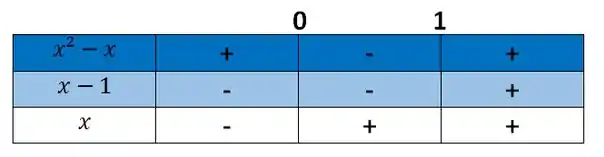
Show?
Então nossa solução será:
Resposta
Exercício Resolvido #5
UPF 2014
As populações de duas cidades, M e N, são dadas em milhares de habitantes pelas funções
Onde a variável t representa o tempo em anos. Após certo instante t, a população de uma dessas cidades é sempre maior do que a da outra. O valor mínimo desse instante t é:
a)-1
b)0
c)2
d)3
e) 4
Passo 1
Vamos supor que a população da cidade M é maior que a população da cidade N. Ou seja
Reescrevendo, temos:
Aplicando as propriedade, temos:
Logo,
Portanto, após 3 anos, a população da cidade M será sempre maior do que a da cidade N
Resposta
Letra D