Inequações Polinomiais
Teoria
A gente já conhece as equações polinomiais, mas se você não lembra a cara dela, vai aí um exemplo de como é essa função,
Repara que temos uma igualdade, mas e as inequações?
Quando falamos de inequações não temos mais uma igualdade, assim como nas equações, mas sim uma desigualdade, agora vão aparecer esses símbolos aqui: .
Vamos separar as equações polinomiais de acordo com os seus graus, nesse tópico vamos falar das equações de primeiro e segundo grau
Inequações do 1º grau
Na inequações do 1° grau, o expoente do é 1 e, em geral, vão aparecer do seguinte modo:
Mas vale lembrar que a desigualdade pode ser qualquer uma dessas aqui:
Resolvendo uma inequação de primeiro grau
Para resolver uma inequação de primeiro grau, precisamos encontrar os valores de que satisfazem a condição da inequação e isso é simples de fazer: basta isolar .
Fácil, não? Se a gente traçar a reta no plano cartesiano, teremos:
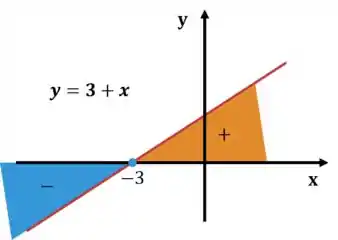
Como queremos , os valores que satisfazem a inequação são os que estão em laranja na figura acima.
Falta uma coisinha na qual você precisa ficar atento. Se o tiver coeficiente negativo, como em:
Você corretamente fará:
Mas ficará atentando a multiplicar os dois lados por e pode concluir que:
Isso, gafanhoto, está ERRADOOOO!
Ao trocarmos o sinal da inequação invertemos a desigualdade!
Dessa maneira, ao multiplicarmos , obtemos, na verdade:
Essa você já não erra mais ;-)
Inequações do 2º grau
Vamos pensar agora em uma inequação com essa cara aqui:
Já aprendemos como resolver equações e sabemos que as funções do 2º grau sempre formam uma parábola.
Ok, mas por que isso é importante?
Quando temos uma inequação, qualquer que seja ela, estamos interessados em saber aonde ela será positiva ou negativa...
Show, mas como vamos resolver isso?
Vamos nessa!
Passo 1
Encontrar as raízes
Ou seja, vamos encontrar os valores onde a nossa equação é igual a zero. Obs: Não precisa se desesperar, nada mais é do que o processo que fazíamos antes, relaxaaaaa rs
Para a nossa equação de exemplo, teremos:
As raízes para essa equação serão:
Esses são os pontos onde o nosso gráfico encosta no eixo x.
Obs: Quando o valor do for negativa a nossa função será ou toda positiva ou toda negativa. Pois não teremos raízes reais. Ok?
Passo 2
Determinar o crescimento da função
No nosso caso, como , a função será crescente.
Passo 3
Estudo de sinais no gráfico.
Observe um esboço do gráfico de nosso exemplo. (Quando você for fazer, pode ser algo assim também, não há necessidade de um gráfico muito rebuscado, cheio de detalhes).
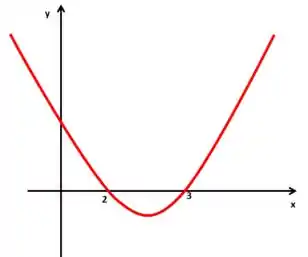
Show?
Muito bem, agora nós vamos marcar nesse gráfico os lugares onde essa função é positiva e onde ela é negativa. Nada de outro mundo, o que estiver para cima do eixo , é positivo, o que estiver para baixo do eixo , negativo.
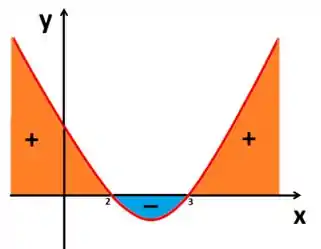
Beleza, através dessa imagem, observamos que nossa função é (negativa) para os valores que estão entre 2 e 3.
Para ficar mais “elegante”, vamos escrever nossa solução assim ó:
Também podemos representar essas respostas atráves de intervalos reais, da seguinte forma:
Esses parênteses ou essas chaves vão indicar que não estamos incluindo nem o 2 e nem o 3 na nossa solução. OMG, qual das duas representações eu utilizo?
Fica a cargo do leitor hahahaha
As duas estão corretas, pode usar a que você achar mais bonitinha :D
E se tivéssemos o no lugar do na nossa inequação?
A nossa solução incluiria os valores onde o será igual a 0 (Ou seja, as nossas raízes).
Se tivéssemos a seguinte inequação, por exemplo:
A nossa resposta, seria os valores em que o , ou seja:
Em termos de intervalos reais, teríamos:
Muita atenção, para incluir o um número na resposta, colocamos o colchete virado pro lado onde ele está fechado.
Belezinha?
Agora é só partir para os exercícios =D
Resolvendo uma inequação de primeiro grau
Inequações do 2º grau
Passo 1
Passo 2
Passo 3
Exercícios Resolvidos
Exercício Resolvido #1
UFF, Cálculo IA-Lista 1, GMA, 2008-1, 1
Resolva a inequação:
Passo 1
Vamos resolver essa inequação, primeiro temos que passar tudo com para o lado esquerdo:
Passando também o que não tem pra direita:
Passo 2
Arrumando:
Agora dividindo tudo por (atenção: quando se divide por um número negativo tem que inverter o sinal da inequação!):
Resposta
Exercício Resolvido #2
Vestibular PUC-RJ 2008
Determine a soma dos números inteiros que satisfazem .
Passo 1
Opa! Duas inequações?! Calma, calma. É só analisarmos cada uma e pegar a interseção entre os conjuntos solução.
Para a primeira, temos:
Isolando :
Passo 2
Agora, para a segunda:
Isolando :
Passo 3
Agora, o resultado final será a interseção dos dois conjuntos solução, ou seja, o conjunto de valores que satisfaz ambas condições.
Para a primeira, precisamos que e a segunda exige . O que satisfaz ambos ao mesmo tempo?
Pois precisa ser maior ou igual a e menor ou igual a . Essa é a nossa solução.
Passo 4
Não terminou ainda não! O problema está pedindo a soma dos números inteiros que compõem a solução. Essa soma é justamente:
Resposta
Exercício Resolvido #3
Elaboração Própria
Quantos números inteiros e positivos satisfazem a inequação
Passo 1
Primeira coisa que vamos fazer, é deixar essa inequação mais amigável, parecida com o que estamos acostumados a resolver. Para isso, vamos fazer o mmc:
Agora, se liga nisso:
Certo? Isso porque estavam todos com o denominador em comum... Dessa forma, podemos multiplicar os dois lados da desigualdade por :
E, assim:
Beleza? Agora, vamos isolar o :
Passo 2
Os números inteiros e positivos que satisfazem essa inequação serão somente o 1 e o 2.Obs.: O zero não é considerado um número positivo e nem um número negativo, ele é neutro.
Portanto, somente dois números satisfazem a inequação.
Resposta
Apenas dois números inteiros e positivos: 1 e 2.
Exercício Resolvido #4
Elaboração Própria
Encontre o conjunto solução para a inequação abaixo:
Passo 1
Fizemos uma parecida na teoria, lembra?
Vamos primeriamente tentar encontrar as raízes da equação. Simbora?
Opaaa! O é negativo, isso significa que não temos raízes reais.
E AGORA? QUEM PODERÁ NOS DEFENDER?
Passo 2
Olhando para o valor do a, vemos que ele é maior do que zero. Isso significa que a nossa função sempre será positiva. O esboço do nosso gráfico vai ficar assim, ó:
Como no enunciado queríamos os valores de x que tornam essa equação negativa, a resposta será: NENHUM rs
Ou seja, o conjunto solução será:
Obs: Ø Conjunto vazio
Resposta
Exercício Resolvido #5
UFF, Cálculo IA-Lista 1, GMA, 2008-1, 8
Resolva a inequação:
Passo 1
Beleza, primeiramente vamos distribuir o termo elevado ao quadrado:
Substituindo, temos:
Jogando tudo para o mesmo lado sem pudor algum:
Opa, temos uma inequação de segundo grau limpinha agora!
Passo 2
Vamos achar as raízes, para então fazer o estudo do sinal:
Logo:
Passo 3
A partir disso, dividimos o domínio em intervalos limitados pelas raízes e testamos o sinal, que só muda quando passa na raiz, ou seja, podemos escolher qualquer valor nos intervalos gerados que garantiremos que o sinal não muda naquele intervalo. Eles serão:
Para o primeiro intervalo, podemos escolher :
Logo, ela é positiva nesse intervalo.
Para o segundo, podemos escolher o :
Logo, ela é negativa nesse intervalo.
Para o terceiro, podemos escolher :
Logo, ela é positiva nesse intervalo.
Passo 4
Voltando a inequação do problema, temos:
Queremos, portanto, o intervalo com valor negativo da expressão, ou seja:
A solução será, portanto:
Resposta
Exercício Resolvido #6
Elaboração Própria
Resolva a inequação
Passo 1
Vamos lá!! Para encontrar a solução da inequação
Precisamos isolar o de um lado da equação. Beleza?!
Passo 2
Para isso, primeiro vamos passar o para o lado direito da desigualdade. Assim,
Agora vamos dividir os dois lados da desigualdade por .
Atenção agora!!!
Algo muito importante de lembrar é quando dividimos por um número negativo precisamos inverter o sinal da inequação!!!
Assim,
Fazendo a divisão, temos
Beleza?!
Resposta
Exercício Resolvido #7
Elaboração Própria
Qual das inequações abaixo aceita o número 2 como solução?
Passo 1
EPAAAAAA, bora lá?! Queremos verificar qual das opções que temos aceita o número 2 como solução. Como então podemos verificar? Basta substituirmos o valor nas inequações e ver se a desigualdade será verdadeira ou não!
Passo 2
Vamos começar então pela inequação da letra (a) ! Substituindo o valor , teremos
Sabemos que , então temos que a desigualdade é falsa, pois 1 não é maior que !
Show de bola?!
Passo 3
Na letra (b) temos a inequação . Vamos seguir o mesmo raciocínio! Substituindo ne inequação, temos
O que não é verdade também, pois 5 é maior que -2!
Passo 4
Vamos continuar com o mesmo raciocínio na letra (c) e (d)! Na inequação , ao substituirmos temos
OPAAAAA! Essa desigualdade é verdadeira, pois 3 é menor do que 4!!! Então já achamos a nossa resposta, mas vamos verificar a letra (d) se também será verdadeira a desigualdade?
Na inequação , ao substituir o valor temos
É... não é verdade essa desigualdade, então 2 não é solução dessa inequação!
Portanto, a nossa resposta é a letra (c)!
Resposta
Exercício Resolvido #8
Elaboração Própria
Se é uma solução da inequação , então
Passo 1
VAMO TIMEEEE!!! Para resolver essa inequação precisamos isolar o ! Para isso, vamos passar o do lado direito da desigualdade para o lado esquerdo
Somando os termos que possuem temos
Show de bola?!
Passo 2
Agora vamos passar o para o lado direito da desigualdade
E por último dividimos ambos os lados da desigualdade por 2
Assim,
Beleza?!
Portanto, a nossa resposta é a letra (b)
Resposta
Exercício Resolvido #9
Elaboração Própria
O triplo de um número somado a é menor que o seu dobro subtraído de . Esse número é necessariamente:
- Maior que
- Maior que
- Igual a
- Menor que
Passo 1
FALA AÍÍÍ!!! Primeiro passo pra resolver esse problema é entender o que o enunciado quer dizer e escrever isso no “matematiquês”, beleza?!
Então vamos lá!! O enunciado diz pra gente: “O triplo de um número somado a é menor que o seu dobro subtraído de ”. Vamos chamar esse número desconhecido de ! Assim,
Ouuuu seja, a nossa inequação é !!
Show de bola?!
Passo 2
Agora isolar o para encontrar o seu valor! Primeira passaremos o para o lado esquerdo da desigualdade
Da mesma forma, passaremos o para o lado direito da desigualdade
Fazendo as continhas, temos
Portanto, a nossa resposta é a letra (d)
Resposta
Exercício Resolvido #10
Elaboração Própria
A soma do dobro de um número somado com 3 é maior que a diferença entre seu quádruplo menos 1. Este número pode ser:
- 1
- 2
- 3
- 4
Passo 1
Vamos lááá!! Primeiro passo pra resolver esse problema é entender o que o enunciado quer dizer e escrever isso no “matematiquês”, beleza?!
O enunciado diz pra gente: “A soma do dobro de um número somado com 3 é maior que a diferença entre seu quádruplo menos 1.”. Vamos chamar esse número desconhecido de ! Assim,
Ouuuu seja, a nossa inequação é
Show de bola?!
Passo 2
Agora isolar o para encontrar o seu valor! Primeira passaremos o para o lado esquerdo da desigualdade
Da mesma forma, passaremos o para o lado direito da desigualdade
Agora dividiremos ambos os lados por . Lembrando que quando dividimos por um número negativo precisamos inverter o sinal da inequação!!!
Portanto, analisando as alternativas, o único valor que é menor que é o 1. Nossa resposta então é a letra (a)