Teorema da Convergência de Fourier
Produzido por Carolina SabaTeoria
Introdução
Já vimos que a série de Fourier é uma representação de funções que a gente não gosta em soma de senos e cossenos (que a gente ama na verdade). Mas será que sempre podemos dizer que a série de Fourier:
É igual à função ? Ou seja, em qualquer ponto eu posso recuperar o valor da função só com aquele somatório maroto?
Vamos ver que sim e não ao mesmo tempo! Quem nos responderá será o tal do teorema de convergência de Fourier.
Funções contínuas por partes
Antes de começar a falar desse Teorema propriamente dito, eu gostaria de relembrar contigo o que é uma função desse tipo.
Uma função é dita ser contínua por partes (ou descontínua por pulos), se em alguns pontos ela “salta” pra outro valor e volta a ser contínua depois disso, veja um exemplo:
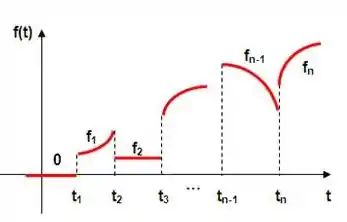
Perceba que , e por aí vai, são todos pontos de descontinuidades por pulos!
As funções que vamos trabalhar aqui serão geralmente funções periódicas, mas com alguma descontinuidade por pulos. Por exemplo, a função periódica :
De período igual a , pode ser desenhada como abaixo:
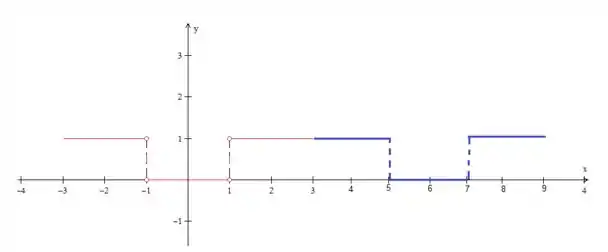
Nela desenhamos apenas dois períodos (um em vermelho e outro em azul), mas já deu pra perceber que ela é descontínua por pulos.
O Teorema na Prática...
Esse teorema da convergência de Fourier nos diz o seguinte:
“A série de Fourier é igual à função onde a função for contínua.”
Então, beleza! Nos trechos contínuos, a série vai ser a própria função no ponto, como desenhado:
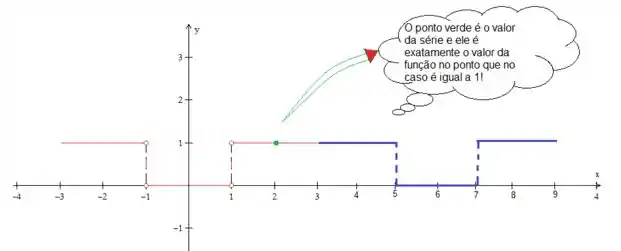
Já no caso das descontinuidades, o teorema nos fala que...
“Mas em pontos de descontinuidade, a série assume o valor do ponto médio da descontinuidade.”
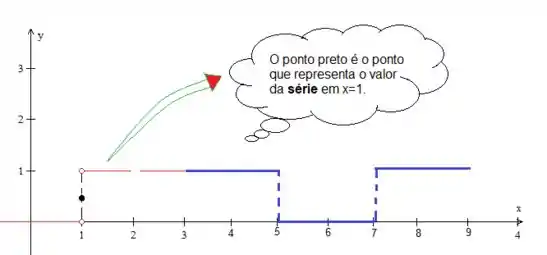
Então, em , por exemplo, temos uma descontinuidade, certo? Ora a função é (pela esquerda) e ora ela passa a ser (a direita). E aí eu te pergunto, qual é o ponto médio? , não concorda? Afinal:
Generalizando o Teorema
De uma forma geral e mais elegante, a gente pode falar isso aqui:
“Seja uma função periódica seccionalmente contínua em , então a Série de Fourier converge para todo real e converge da seguinte forma”
OBS: e são os limites laterais de no ponto : é o limite lateral pela direita e limite lateral pela esquerda.
Mas ATENÇÃO: A série tende para (média da descontinuidade) apenas em pontos de descontinuidade!
Na prática, meu amigo, é exatamente o que fizemos! Em pontos de continuidade, é a própria função. E em casos de descontinuidade (como no nosso ), basta pegar o valor da função a direita (), somar com o da esquerda () e dividir por (tirar a média):
Partiu então exercícios?
Funções contínuas por partes
O Teorema na Prática...
Generalizando o Teorema
Exercícios Resolvidos
Exercício Resolvido #1
William E. Boyce e Richard C. DiPrima, Equações diferenciais elementares e problemas de contorno, 9ª ed., Rio de Janeiro: LTC, 2010, pp. 317. Exercício 2
Suponha que a função dada é estendida, periodicamente, para fora do intervalo original.
- Encontre a série de Fourier da função estendida
- Esboce o gráfico da função para qual a série converge por três períodos
Passo 1
Letra a)
Precisamos encontrar a Série de Fourier de , temos o seguinte:
Como o intervalo da função que o problema deu é (de até ) e temos que estender a função, esse será o seu período. Então:
Passo 2
Agora vamos calcular
Fazendo na expressão de temos:
Veja que de a temos duas expressões diferentes para , então o único jeito é dividir essa integral em duas, olha só:
Repare nos intervalos que escrevemos! A função vale em e em . Resolvendo essas integrais, temos
Passo 3
Agora vamos calcular os outros ’s. Temos que:
Dividindo essa integral, como fizemos com :
Agora vamos integrar por partes, ok? Fazendo
Agora vamos analisar com calma. Perceba que
Logo
Guarde isso!
Passo 4
Agora só falta calcular os ’s
Dividindo essa integral:
Agora vamos fazer a integração por partes:
Lembrando que
Temos
Passo 5
Agora vamos substituir tudo o que encontramos, temos:
Vamos separar a série em duas para ver melhor:
Agora vamos com calma. Não podemos escrever direto no somatório porque isso só vale para ímpar. Vamos definir então , porque isso garante que temos índices ímpares, ok? Para temos , portanto a série deve começar em .Temos então
Agora vamos substituir o valor de usando a notação também, só para ficar igual à primeira série
Já que as duas séries possuem os mesmos índices, podemos juntá-las, não é?
Passo 6
Letra b)
Certo, agora só falta o gráfico. Essa questão é bem simples, mas você tem que ter muito cuidado com a falta de atenção. O enunciado pede para desenharmos o gráfico da função para qual a série converge. Ah, é só desenhar a função do enunciado, né?
Não! O que você vai fazer nesse tipo de questão é o seguinte:
- Desenhar as informações sobre que o enunciado dá nos colchetes (em vermelho)
- Repetir essa para a esquerda e para a direita ignorando os pontos de descontinuidade (em azul);
- Fazer a média dos limites laterais em cada ponto de descontinuidade (em preto)
Porque isso? Por causa daquele Teorema da Convergência de Fourier que diz que a soma da série de Fourier de converge para onde a função é contínua (por isso nós copiamos essas retas do enunciado) e converge para a média dos limites laterais nos pontos de descontinuidade. Por exemplo, para , a soma da série converge para:
Lembre-se de fazer pontos preenchidos quando representar essas médias (em preto) e pontos “vazios” (em azul e vermelho) nos limites laterais.
Portanto, esse gráfico que fizemos não representa , mas a soma da sua série de Fourier, ok? Claro que a soma da série é muito parecida com a função.
Obs: Se a função periódica for toda contínua, a soma da série converge para em todos os pontos.
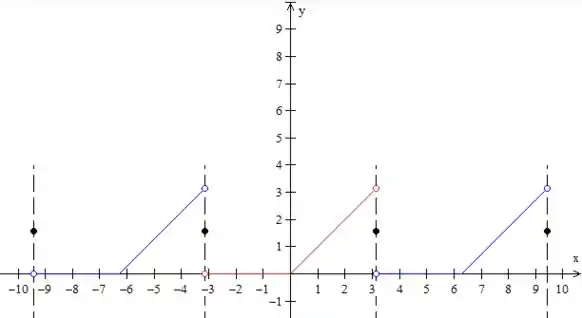
Resposta
Exercício Resolvido #2
UNICAMP - Cálculo 3 - P3 2011.1 - 3b,c
Seja a função dada por
Construa a extensão par e periódica de para toda a reta , com período , e calcule a série de Fourier desta extensão.
Quanto vale esta série nos pontos e ?
Não esqueça a justificativa.
Tomando , calcule o valor da série
Passo 1
Para calcular a série de Fourier, primeiro identificamos o período . Isto é, . Portanto, .
A extensão par é obtida espelhando-se a função:
Passo 2
A série é dada por cossenos (já que ela é par):
Vamos avaliar os coeficientes da série:
Passo 3
Para o termo geral , temos:
Vamos resolver logo por integração por partes...
Passo 4
Então, temos o seguinte:
Passo 5
Mas sabemos que
Vamos obter
Passo 6
Agora note que para par, o seno se anula; para ímpar é o cosseno que se anula.
E, assim, temos:
Passo 7
Nos pontos e , a série converge para:
Passo 8
Vamos tomar :
Agora veja que se for ímpar, o cosseno é zero. Então vamos tomar só os casos em que seja par:
Mas é par, isto é, , :
Passo 9
De novo, olha aí que , então o termo
será
Aí fica assim: .
Passo 10
Mas como vimos que, em , a série converge para , teremos:
E basta trocar por para vermos que o somatório que buscamos se iguala a .
Resposta
Extensão:
Série de Fourier: ;
; .
Exercício Resolvido #3
USP - Cálculo 4 - P2 2012 - 2b
Seja
a)Determine a série de Fourier de senos de
b)Mostre que a série de Fourier de senos de converge para uma função e esboce o gráfico da função em
c)Determine
Passo 1
a)Calma galera, você pode estar pensando, mas cara, essa função é par!!! Como fazer ela como uma série de Fourier de seno se essa série só existe pra função ímpar? Mas opa, ele só definiu a função de , se a gente definir em , pronto esse moleque é ímpar!
Bem bem, a série de Fourier de seno é:
]
:
A segunda integral vamos resolver de forma indeterminada primeiro, ela é maiorzinha:
Vamos fazer uma integração por partes:
Assim fica:
Agora para resolver essa outra integral, novamente outra integração por partes:
Então simbora:
Desenvolvendo:
Então vimos que:
Substituindo:
Mas:
Assim finalmente:
]
E com isso a série de Fourier de seno fica definida:
Passo 2
b)A extensão dessa função é seccionalmente contínua, e seccionalmente de classe , logo pelo teorema de convergência da série de Fourier, esta série converge a toda extensão em , exceto nos pontos de descontinuidade!
Então a função fica assim:
E é só repetir o período que não tem erro!
O gráfico ficou:
Passo 3
c)
Ae tu fica, “É clã, soldado morreu na trincheira” Mas calma, lembra que isso é uma função periódica e uma função ímpar, a cada 1 período a área necessariamente tem que dar zero!, vamos reescrever isso:
Para facilitar mais ainda, podemos tirar mais coisa:
Mas opa, a gente viu que dentro de a função que rege isso é:
Logo:
Resposta
a)
b) A extensão dessa função é seccionalmente contínua, e seccionalmente de classe , logo pelo teorema de convergência da série de Fourier, esta série converge a toda extensão em , exceto nos pontos de descontinuidade
c)