Exercícios de Teorema da Convergência de Fourier - Lista de Exercícios Resolvida
Questão 1
Suponha que a função dada é estendida, periodicamente, para fora do intervalo original.
- Encontre a série de Fourier da função estendida
- Esboce o gráfico da função para qual a série converge por três períodos
Questão 2
Seja
a)Determine a série de Fourier de senos de
b)Mostre que a série de Fourier de senos de converge para uma função e esboce o gráfico da função em
c)Determine
Ver solução completaQuestão 3
Seja a função dada por
Construa a extensão par e periódica de para toda a reta , com período , e calcule a série de Fourier desta extensão.
Quanto vale esta série nos pontos e ?
Não esqueça a justificativa.
Tomando , calcule o valor da série
Ver solução completaQuestão 4
Seja a função definida por
- Determine a série de Fourier de
- Esboce o gráfico da série de Fourier obtida no item (a) no intervalo [-6,6]
Questão 5
a) Calcule a série de Fourier da função
b) Encontre a soma da série
Utilizando o item
Ver solução completaQuestão 6
Teste 3: Sejam uma função periódica de período tal que para e para , e a soma da sua série de Fourier. Então , e valem, respectivamente:
Questão 7
Dada a função
a) Determine a série de Fourier de
b) Esboce o gráfico da série de Fourier de obtida no item (a) no intervalo .
c) Calcule a soma
Ver solução completaQuestão 8
Seja uma função ímpar, contínua, por partes com e cujo gráfico no intervalo está esboçado a seguir
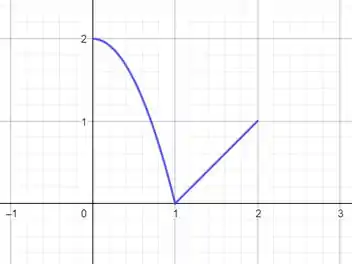
Sendo sua série de Fourier, analise as afirmações a seguir:
Podemos afirmar que:
Apenas e são verdadeiras
Apenas e são verdadeiras
Apenas e são verdadeiras
Todas as afirmações são verdadeiras
Nenhuma afirmação é verdadeira
Ver solução completaQuestão 9
Questão 7: Seja
A série de Fourier da função , periódica de período , definida por
E seja sua soma. Podemos afirmar que:
- para todo .
- .
- apenas se .
- .
- para todo inteiro .
Questão 10
Questão 4: Seja , para e para . Denotamos por a soma da série de senos da função . Quais são os valores de ?
Questão 11
Teste 11: Seja para e a soma da série de cossenos de . No intervalo , é dada por:
Questão 12
Teste 12: Seja a função
A soma da série de Fourier de no intervalo é:
Questão 14
Seja
Sem calcular a série de Fourier (use o Teorema de Fourier), responda: para que valor a série de Fourier converge em ? (Não esqueça a justificativa.)
Calcule a séire de Fourier da função .
Tomando deduza o valor da soma
Ver solução completaQuestão 16
Considere a função definida no intervalo .
Use o resultado do item para mostrar que
Justifique usando o teorema de Fourier.
Ver solução completaQuestão 17
Suponha que é uma função contínua com derivada contínua por partes.
Se , sob quais condições coincide com sua série de Fourier em senos para todo satisfazendo
Ver solução completaQuestão 18
Suponha que é uma função contínua com derivada contínua por partes.
Se , sob quais condições coincide com sua série de Fourier em cossenos para todo satisfazendo
Ver solução completaQuestão 19
Suponha que é uma função contínua com derivada contínua por partes.
Se , sob quais condições coincide com sua série de Fourier para todo satisfazendo
Ver solução completaQuestão 20
Para todas as funções cuja séries de Fourier você calculou nos exercícios e e , e .
Em quais pontos do intervalo vale que ?
Ver solução completaQuestão 21
Para todas as funções cuja séries de Fourier você calculou nos exercícios e e , e .
Explique por que estas funções satisfazem as hipóteses do teorema de convergência das séries de Fourier estudado nesta semana.
Ver solução completaQuestão 22
Para todas as funções cuja séries de Fourier você calculou nos exercícios e e , e .
Esboce o gráfico de no intervalo
Ver solução completaQuestão 24
Teste 13: seja uma função ímpar, por partes, com e cujo gráfico no intervalo está esboçado a seguir:
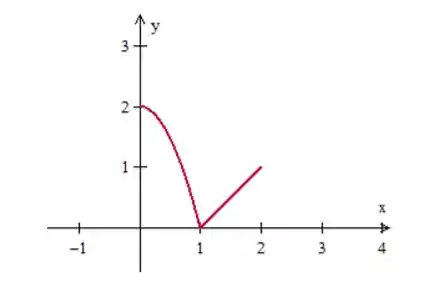
Sendo a soma da sua série de Fourier, analise as afirmações a seguir:
- para todo
- para todo
- para todo
- para todo
Podemos afirmar que:
- Apenas e são verdadeiras.
- Apenas e são verdadeiras.
- Apenas e são verdadeiras.
- Apenas e são verdadeiras.