Ar a 5°C e 70% de umidade relativa é aquecido até 25°C (obs: temperaturas de bulbo seco). A vazão volumétrica é de 50 m3/min (no estado inicial) e a pressão da mistura é P = 100 kPa. Dados: Pressão de saturação a 5°C = 0,872 kPa;
Encontre:
a) A transferência de calor que ocorre durante este processo.
b) A umidade relativa final
Passo 1
A transferência de calor nesse caso (de processo isobárico) é dada por
Então precisamos achar a entalpia dos dois estados (dada pela carta psicrométrica) e a vazão mássica de ar que será encontrada pela equação dos gases na forma
Passo 2
Vamos achar a vazão mássica como mostramos na etapa anterior.
A pressão do ar seco é igual a pressão total menos a pressão do vapor
A pressão do vapor é igual a umidade relativa vezes a pressão de saturação na mesma temperatura
Substituindo os valores encontrados para achar a massa específica
Agora podemos achar a vazão mássica
Passo 3
Neste passo iremos achar as entalpias dos estados 1 e 2. Para isso vamos utilizar a carta psicrométrica. Para o estado 1 temos uma entalpia de e umidade absoluta de aproximadamente .
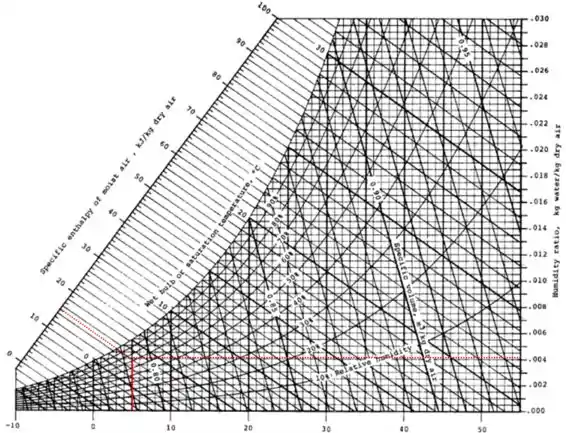
Para o estado 2 vamos ter uma entalpia de e uma umidade relativa de 20%.
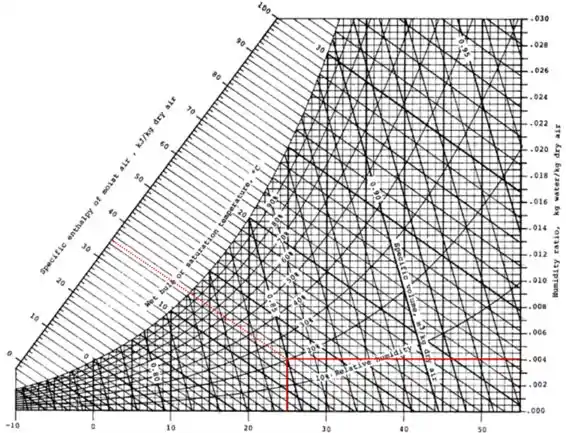
Observe que com duas informações é possível achar um ponto específico na carta e com isso achar os outros valores importantes. No primeiro caso utilizamos a umidade relativa e a temperatura, já no segundo utilizamos a temperatura e a umidade absoluta (que foi retirada do primeiro caso, já que não houve aumento em massa da quantidade de água).
Passo 4
Logo a quantidade de calor é igual a