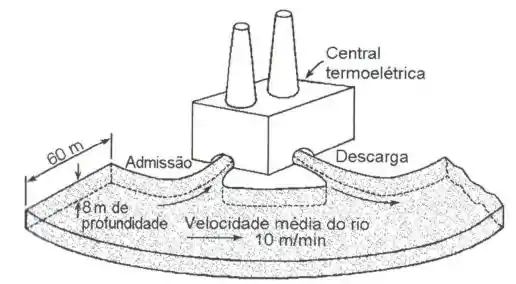
Propõe-se construir uma central termoelétrica com potência de 1000 MW e utilizando vapor e água como fluido de trabalho. Os condensadores devem ser resfriados com água de um rio ver (figura abaixo). A temperatura máxima do vapor será de 550 °C e a pressão nos condensadores será de 10 kPa. Como consultor de engenharia, você é solicitado a estimar o aumento da temperatura na água do rio (entre montante e jusante da usina). Qual é a sua estimativa? Calcule o trabalho necessário para a operação dessa bomba de calor. Considere que a central opere num ciclo de Carnot. Dados:
Passo 1
Primeiro vamos ver os dados que nos foram dados desta questão. Referente à própria central termoelétrica temos:
Com relação ao rio temos os seguintes dados:
- Profundidade = 8 metros.
- Largura = 60 metros.
Para calcular a variação de temperatura temos de estimar a massa que corre no rio e a quantidade de calor rejeitado no rio . Vamos começar calculando .
Passo 2
Como temos a quantidade de trabalho realizado por segundo (), se calcularmos a eficiência deste ciclo poderemos saber , e também , embora não seja relevante neste problema.
Então vamos calcular a eficiência deste ciclo de Carnot que, como sabemos, é fornecida pela equação
Mas agora olha que mas não foi dado. Mas tem o detalhe que, no condensador, a pressão é de 10 kPa, então vamos lá na tabela da água saturada e vemos que a água a pressão de 10 kPa condensa a 45,81°C.
Agora podemos calcular a eficiência, com as temperaturas em Kelvin!
Passo 3
Agora podemos achar o , lembrando que a eficiência também é dada por
Que se dividirmos pelo tempo em cima e embaixo vamos ter uma relação de potência e taxa de transmissão de calor, ao invés de trabalho e calor.
Aqui podemos fazer um pouco de álgebra para eliminar o e achar direto ou, como farei agora, calcular ambos.
Para achar utilizamos a primeira lei da termodinâmica para ciclos (de novo dividindo tudo pelo tempo):
Passo 4
No passo 3 conseguimos achar o calor transferido para o rio por segundo. Com isso vamos calcular a vazão mássica do rio, também por segundo né pra fazer algum sentido! haha.
Lembrando lá de fentran ou mecflu temos que a vazão mássica é dada por
Considerando a massa específica , e temos
Passo 5
Agora ficou facinho, basta fazer o famoso Mr. cat, para calcular a variação de temperatura.
Obs: Aqui vai uma observação legal. Preste sempre atenção nas unidades! Viu que se dividirmos pelo tempo dos dois lados (ou em cima e embaixo como no passo 3) a unidade continua igual e temos uma taxa de alguma grandeza, ou seja, aquela grandeza pelo tempo, que é representado com um pontinho em cima da unidade.