Propriedades Térmicas
Produzido por Erick PinhoTeoria
Opa, bora bater um papo sobre Propriedades Térmicas?!
Quando estudamos as propriedades térmicas de um material a gente avalia o que acontece quando ele é exposto a variações de temperatura! Por exemplo: Como o calor é conduzido? Se eu ceder calor para o meu material, qual vai ser a variação de temperatura? Ele vai dilatar?
São essas questões que a gente vai responder hoje! 😋
📢 Clique para ver mais:
- Propriedades Térmicas: Exercícios Resolvidos
- Propriedades elétricas
- Propriedades ópticas dos materiais
Capacidade Calorífica
A capacidade calorífica
Para fazer esse cálculo, usamos a seguinte fórmula:
Onde
Onde
Opa, então
Expansão Térmica
Quase todas as matérias, podem expandir com o aumento da temperatura e contrair-se quando sua temperatura é reduzida e o efeito da variação de temperatura pode prejudicar dependendo da aplicação dos materiais. Por isso as pontes tem o que chamamos de junta de dilatação!

Se você já passou pela ponte Rio-Niterói você pode ter notado essas “rachaduras” enormes e assustadoras! Essas são as juntas de dilatação, elas permitem que o concreto se expanda no calor e se comprima no frio sem que essa variação de volume cause rachaduras de verdade!
As dilatações podem ser lineares, superficiais e volumétricas! Bora ver cada uma delas?
Dilatação Linear
A dilatação linear considera apenas uma dimensão e usamos a seguinte fórmula para calcula-la:
Onde
Dilatação Superficial
A dilatação superficial considera duas dimensões! Como por exemplo uma chapa fina de metal, ela é um objeto tridimensional, mas como a largura e o comprimento são muito maiores que a espessura, podemos usar a dilatação superficial!
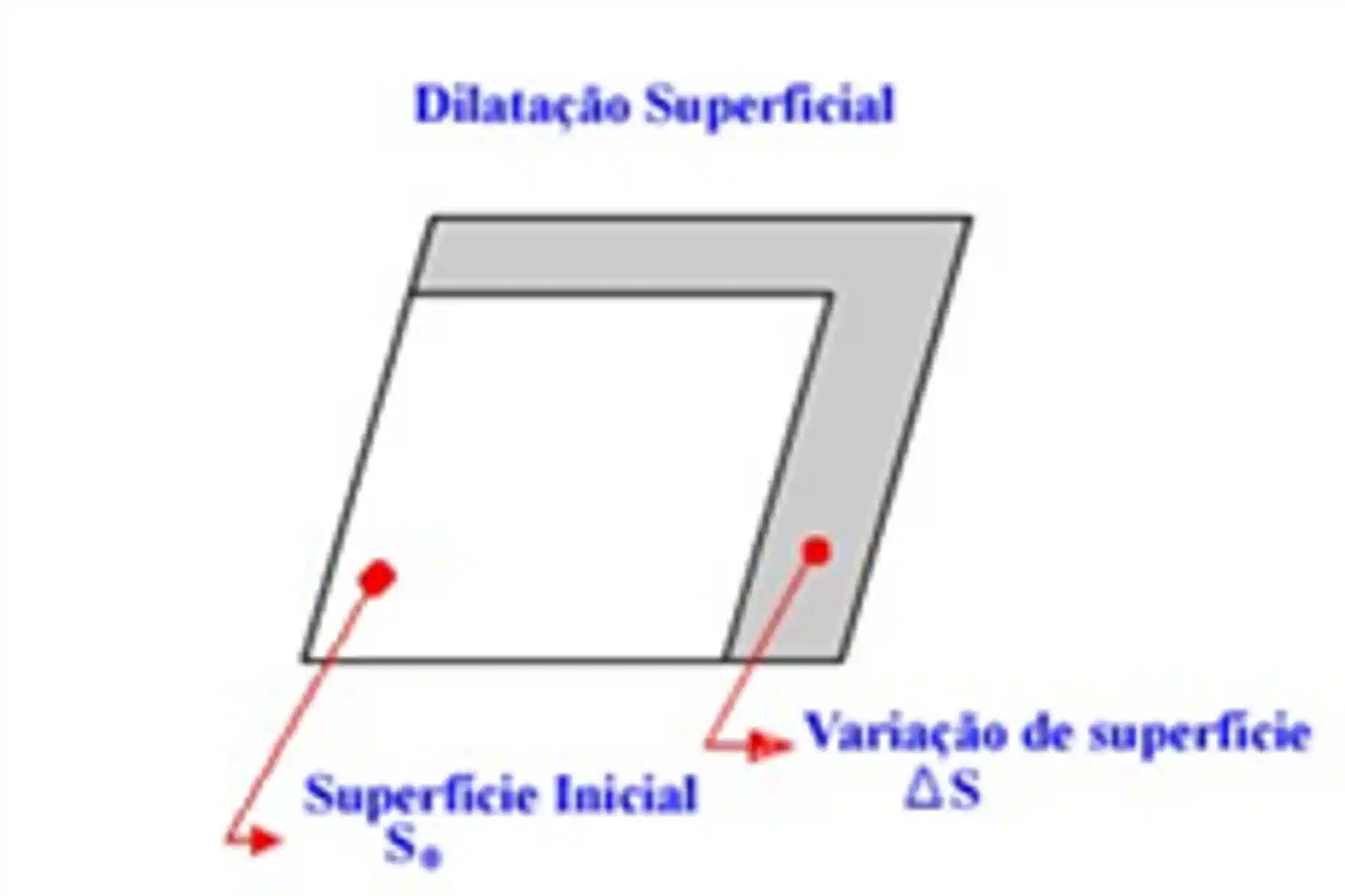
Podemos calcular a dilatação superficial usando a seguinte fórmula:
Aqui o
Dilatação Volumétrica
A dilatação volumétrica considera as três dimensões do objeto: Altura, largura e comprimento:
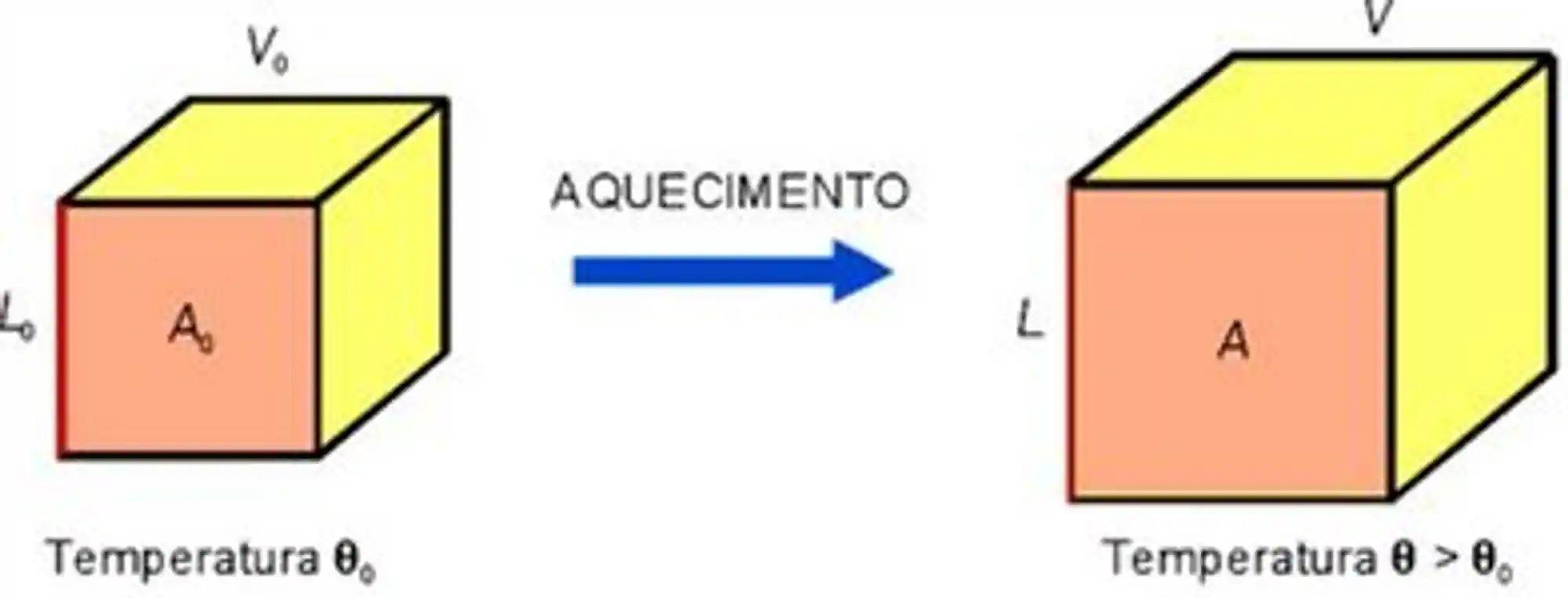
Calculamos a dilatação volumétrica fazendo:
Onde
Condutividade Térmica
A condutividade térmica
Um exemplo de baixa condutividade é o cabo de panela feito de plástico (mau condutor térmico), que evita que o calor do metal seja transferido diretamente a nossas mãozinhas, atuando como um “isolante térmico”.

Materiais com elevada condutividade térmica são empregados como dissipadores de calor e materiais de pequena condutividade térmica são empregados como isolante térmicos. A quantidade de calor que passa por uma área em um dado material é descrito pela seguinte expressão:
Onde
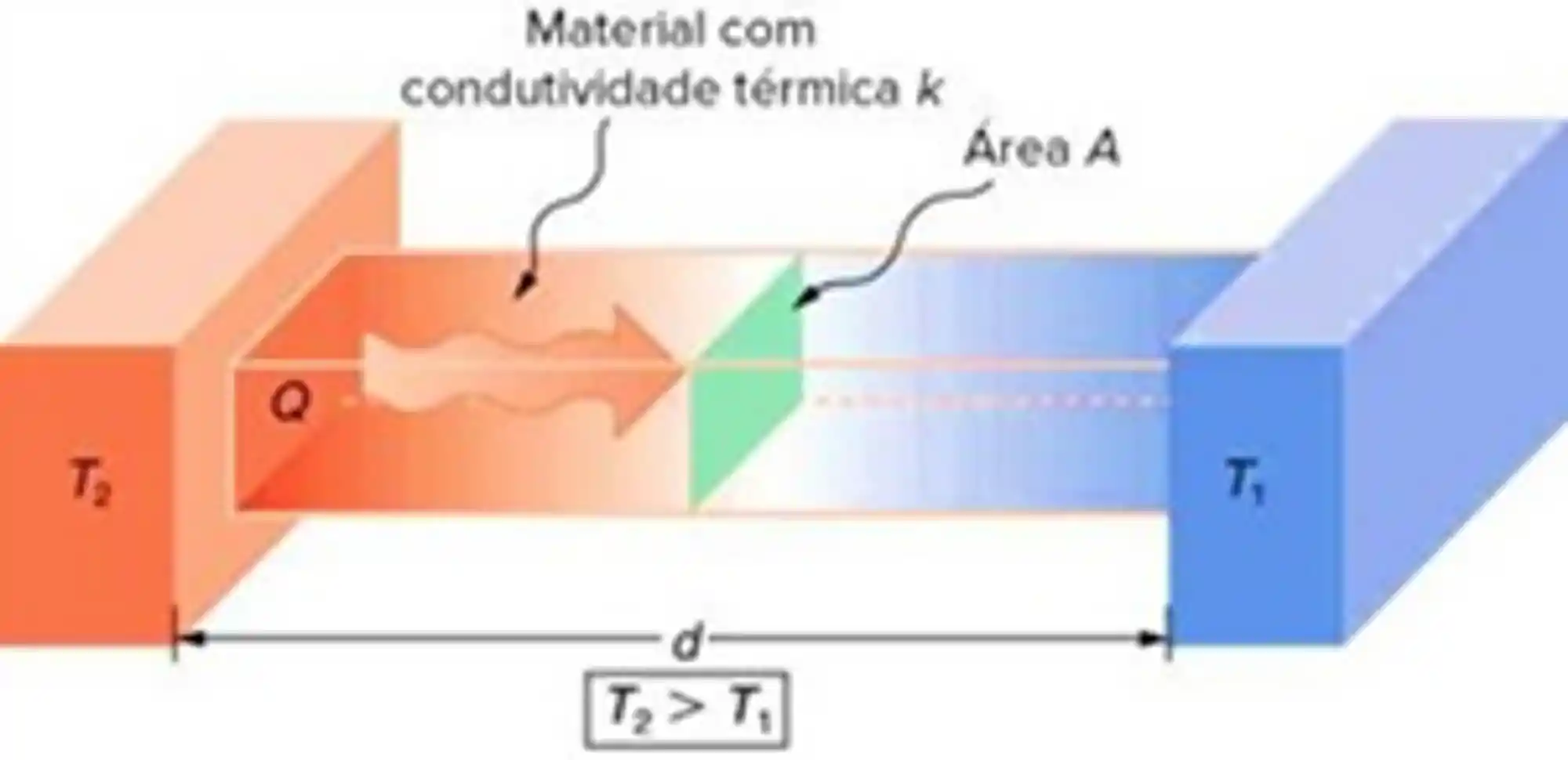
É importante sempre ter em mente que o calor flui da maior temperatura para a menor temperatura!
Agora vamos praticar com exercícios?
Expansão Térmica
Condutividade Térmica
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Analisando o calor específico do cobre é 0,09 cal/g.ºC e o do alumínio 0,22 cal/g.ºC, qual destes materiais necessitará de máxima quantidade de calor fornecida ou removida para que aconteçam as mesmas mudanças de temperaturas?
Passo 1
Compare os valores do calor específico de ambos materiais, notem que o do alumínio é maior
Passo 2
Portanto precisará de maior quantidade de calor fornecida
Resposta
Alumínio
Exercício Resolvido #2
Elaboração própria
Analisando o calor específico da prata é de 0,05 cal/g.ºC e o do ouro 0,03 cal/g.ºC, qual destes materiais necessitará de máxima quantidade de calor fornecida ou removida para que aconteçam as mesmas mudanças de temperaturas?
Passo 1
Compare os valores do calor específico de ambos materiais, notem que da prata é maior
Passo 2
Portanto precisará de maior quantidade de calor fornecida
Resposta
Prata
Exercício Resolvido #3
Elaboração própria
Analisando o calor específico do cobre é 0,09 cal/g.ºC e o do alumínio 0,22 cal/g.ºC, qual destes materiais necessitará de máxima quantidade de calor fornecida ou removida para que aconteçam as mesmas mudanças de temperaturas?
- A lata devido à menor condutividade térmica
- O vidro devido à maior condutividade térmica
- A lata devido à maior condutividade térmica
Passo 1
A lata é feita de alumínio, então primeiramente devemos encontrar sua condutividade térmica, que é de aproximadamente 238 W/(m.k)
Passo 2
A condutividade térmica do vidro é de aproximadamente 0,8 W/(m.k)
Passo 3
Comparando os valores, o maior valor é do alumínio (lata de ceva)
Resposta
Alternativa III
Exercício Resolvido #4
Elaboração própria
Quanto a definição de capacidade calorífica determine a resposta correta:
- A capacidade calorífica de um material é a quantidade de calor necessária para reduzir a sua temperatura e depende do número de materiais.
- A capacidade térmica dos materiais independem da massa do material
- Se ao material for cedida uma quantidade de calor e a sua temperatura variar temos então, a determinação da capacidade térmica do material
Passo 1
A capacidade calorífica de um material é a quantidade de calor necessária para aumentar a sua temperatura e independe do número de materiais
Passo 2
A capacidade térmica dos materiais depende da massa do material
Passo 3
Onde: C (capacidade calorífica), dQ (energia), dt (temperatura) unidades: J/mol.K e cal/mol.K
Resposta
Alternativa III
Exercício Resolvido #5
Adaptado de: https://exercicios.mundoeducacao.bol.uol.com.br/exercicios-fisica/exercicios-sobre-dilatacao-termica.htm
O vidro temperado apresenta maior resistência ao choque térmico do que o vidro comum, assinale a alternativa correta:
- Apresenta alto coeficiente de rigidez.
- Apresenta baixo coeficiente de dilatação térmica.
- Apresenta elevado calor específico.
Passo 1
O vidro é um material frágil, portanto não rígido.
Passo 2
Sua resistência térmica é devido ao baixo coeficiente de dilatação térmica
Passo 3
O vidro pirex apresenta um baixo calor específico quando comparado ao vidro comum
Resposta
Alternativa B
Exercício Resolvido #6
Elaboração própria
Dois fios metálicos 1 e 2, fabricado de diferentes materiais, apresentam o mesmo comprimento e temperatura iniciais. Quando a temperatura acresce para um valor T, os comprimentos de 1 e 2 acrescem 4% e 8%, simultaneamente. Defina a razão aproximada entre o coeficiente de dilatação do fio 1 pelo coeficiente do fio 2.
Passo 1
Primeiramente vamos relembra a fórmula para posteriormente acharmos a razão entre os fios.
ΔL= αLi x ΔT
Passo 2
Agora iremos determinar primeiramente para o fio 1:
0,04 Li = Li . α1 . ΔT
α1 = 0,04/ ΔT
Passo 3
Agora para o fio 2:
0,08 Li = Li . α2 . ΔT
α2= 0,06/ ΔT
Passo 4
Agora para definirmos a razão aproximada entre o coeficiente de dilatação do fio 1 pelo coeficiente do fio 2, basta dividir um pelo outro.
α 1/ α2= 0,04/0,06
α 1/ α2= 0,66
Resposta
0,66
Exercício Resolvido #7
Elaboração própria
Qual será a variação de temperatura de uma barra de ferro para que ela tenha uma expansão linear correspondente a 0,41% da sua dimensão inicial? Atenda o coeficiente de expansão do ferro com o 11 x 10– 6/ ºC.
Passo 1
Primeiramente vamos relembrar a fórmula
ΔL= αLi x ΔT
Sendo coeficiente de expansão (α)= 11 x 10– 6/ ºC
Dimensão inicial (Li)= 0,41%
Passo 2
A dilatação tolerada pela barra é correspondente à porcentagem de aumento, portanto:
ΔL= αLi x ΔT
Δt= ΔL/αLi
Δt= 4,1 x 10-3/11 x 10– 6
Δt= 381,81°C
Resposta
381,81°C
Exercício Resolvido #8
Elaboração própria
De quanto será o aumento percentual no comprimento de uma barra de alumínio, inicialmente a 25°C, quando aquecida até 85°C. Coeficiente de dilatação 25 x 10– 6/ ºC do alumínio.
Passo 1
Primeiramente vamos relembrar a fórmula
ΔL= αLi x ΔT
Sendo coeficiente de expansão (α)= 25 x 10– 6/ ºC
Variação da temperatura Δt= 85-25= 60°C
Passo 2
A dilatação tolerada pela barra é correspondente à porcentagem de aumento, portanto:
ΔL= αLi x ΔT
ΔL= Li x25 x 10– 6 x 60
ΔL= 1,5 x 10-3 Li
Agora temos que encontrar o percentual de dilatação
0,15 x 10-2 Li= (1,5/100) x Li
ΔL= 0,15%
Resposta
0,15%