Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 3.Perguntas e Problemas - Ex. 9

Calcule o raio de um átomo de vanádio, dado que o V possui uma estrutura cristalina CCC, uma massa específica   5,96 g / c m ³ e um peso atômico 50,9   g / m o l .

Passo 1

Pra calcular o raio atômico a gente vai ter que usar as informações que temos de massa específica e peso pra chegar no volume da célula unitária. À partir daí conseguimos encontrar o raio usando as relações conhecidas entre a aresta e o raio atômico da estrutura CCC!

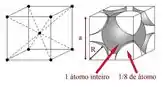
Olhando pra imagem da estrutura CCC a gente pode calcular que uma célula unitária contém 2 átomos: 8   x   1 8 + 1 !

Passo 2

Pras nossas unidade fecharem direitinho, precisaremos usar a relação de Avogadro que diz que em 1 mol de moléculas existem 6,023   x   10 23 partículas! 50,9   g m o l ÷ 6,023   x   10 23 p a r t í c u l a s m o l = 50,9     g m o l x 1 6,023   x   10 23 m o l p a r t í c u l a s

1   p a r t í c u l a = 8,451   x   10 - 23 g  

Como em uma célula temos 2 átomos, então a massa total em uma célula unitária é:

m = 16,902   x 10 - 23 g Finalmente vamos calcular o volume! ρ = m V = 5,96   g c m ³   V = 16,902   x 10 - 23 5,96 = 2,836   x   10 - 23   c m ³

Passo 3

Como temos que   V = a 3 = 2,836 x   10 - 23   c m 3 .

Convertendo 1   c m = 10 7 n m → V = 0,02836   n m ³ .

Tirando a raiz cúbica pra achar a , temos que a = 0,305   n m

Passo 4

Na estrutura CCC, como podemos ver na figura lá em cima, podemos relacionar os raios das esferas com a diagonal principal do cubo. Usando a seguinte relação:

4 r = a 3

Finalmente, calculando o raio usando a relação temos que:

r = 0,132   n m

Resposta

r V = 0,132   n m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Explique por que as propriedades dos materiais policristalinos são, na maioria das vezes, isotrópicas.
A figura a seguir mostra os esquemas de empacotamento atômico para várias direções cristalográficas diferentes de um metal hipotético. Para cada direção, os círculos representam apenas os átomos conti
Converta os planos (010) e (101) ao sistema de quatro índices de Miller-Bravais para células unitárias hexagonais.
A figura a seguir mostra três planos cristalográficos diferentes para uma célula unitária de alguma metal hipotético. Os círculos representam os átomos.A qual sistema cristalino pertence a célula unit
Desenvolva expressões para a densidade linear em termos do raio atômico R para as direções [110] e [111] na estrutura CCC.Calcule e compare os valores da densidade linear para essas mesmas duas direçõ