Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 3.Perguntas e Problemas - Ex. 4
Mostre que a razão ideal ideal é de 1,633, para a estrutura cristalina HC.
Passo 1
Para a estrutura hexagonal compacta, chamamos de a distância entre os átomos da “tampa” e a altura da estrutura, conforme o desenho a seguir:
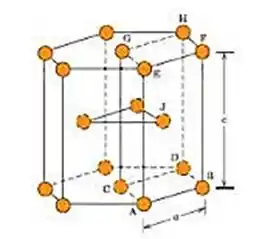
A razão ideal seria onde os átomos estivessem na sua configuração mais compactada possível.
Para encontrar essa razão vamos usar relações trigonométricas e semelhança de triângulo, conforme as figuras a seguir:
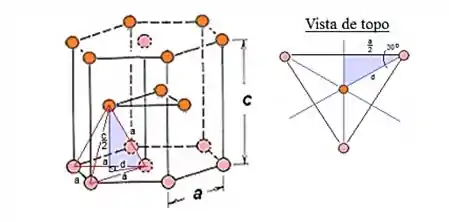
Passo 2
Primeiro temos que encontrar o valor de usando trigonometria:
Passo 3
Agora vamos encontrar a relação entre a e c usando o Teorema de Pitágoras:
Resposta
, como queríamos demonstrar!
Exercícios de Livros Relacionados
A partir dos dados na Tabela 12.3, calcule a massa específica teórica do C a F 2 , com estrutura da fluorita.
A célula unitária para o C r 2 O 3 apresenta simetria hexagonal com os seguintes parâmetros da rede cristalina: a = 0.4961 n m e c = 1.360 n m . Se a massa específica desse material é de 5.22 g / c m
O óxido de magnésio tem a estrutura cristalina do sal-gema e uma massa específica de 3.58 g / c m 3 . Determine o comprimento da aresta da célula unitária.Como esse resultado se compara ao comprimento
Calcule a massa específica teórica do diamante dado que a distância C-C e o ângulo de ligação são de 0.154n m e 109.5 º º, respectivamente. Como esse valor se compara à massa específica medida?
Para cada uma das seguintes estruturas cristalinas, represente o plano indicado do modo feito nas Figuras 3.11 e 3.12, mostrando tanto os ânions quanto os cátions:plano (100) para a estrutura cristali