Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 8.Perguntas e Problemas - Ex. 31
Um componente cilindrico construido a partir de uma liga S- possui um diâmetro de . Determine a carga máxima que pode ser aplicada para que esse componente sobreviva a ).
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Para analisar a figura , temos que identificar o tempo de vida até a ruptura que é de e marcar o ponto que intercepta a curva correspondente a .
Lembrando que em notação científica é igual a .
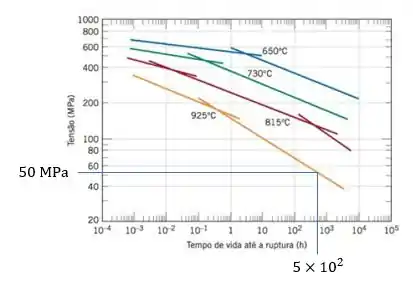
Passo 2
De acordo com a figura , o valor de tensão corresponde a aproximadamente . Como queremos a carga máxima, e sabendo que esta é dada pelo produto entre a tensão e a área da seção transversal, temos que:
Como a área de uma seção circula é dada por:
Temos que:
Substituindo os valores, temos que:
A carga máxima será:
Resposta
Exercícios de Livros Relacionados
Os dados obtidos para a fluência estacionária de um aço inoxidável sob um nível de tensão de 70M P a ( 10.000p s i ) são os seguintes:Se o valor do expoente de tensão n para essa liga é 7,0 , calcule
Considere um componente da liga S- 590 (Figura 8.32 ) que está submetido a uma tensão de 200M P a ( 29.000p s i ). Em qual temperatura o seu tempo de vida até a ruptura será de 500h ?
Um componente de liga S- 590 (Figura 8.32 ) deve possuir um tempo de vida até a ruptura por fluência de pelo menos 100 dias a 500 ° C( 773K ) . Calcule o nível máximo de tensão admissível.
Para um aço inoxidável 18 - 8 Mo (Figura 8.35 ), estime o tempo de vida até a ruptura para um componente que está submetido a uma tensão de 80M P a ( 11.600p s i ) a 700 ° C( 973K ) . Figura 8.35 Loga
Considere um componente de aço inoxidável 18 - 8 Mo (Figura 8.35 ) que está exposto a uma temperatura de 500 ° C( 773K ) . Qual é o nível máximo de tensão admissível para um tempo de vida útil até a r