Os dados obtidos para a fluência estacionária de um aço inoxidável sob um nível de tensão de () são os seguintes:
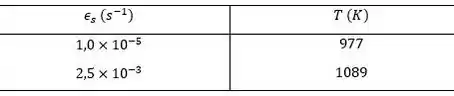
Se o valor do expoente de tensão para essa liga é , calcule a taxa de fluência estacionária a e sob um nível de tensão de ().
Passo 1
Olá! Tudo bem? Neste exercício, devemos determinar a taxa de fluência estacionária a e sob um nível de tensão de (). Assim, para esse problema, tomando os logaritmos naturais de ambos os lados da Equação , obtém-se:
Com os dados fornecidos, há duas incógnitas nessa equação e . Usando os dados fornecidos no enunciado, podemos configurar duas equações independentes da seguinte maneira:
Passo 2
Agora, resolver simultaneamente e leva a e . Assim, agora é possível determinar a taxa de fluência estacionária a e sob um nível de tensão de , usando a Equação .