Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 8.Problemas de Projetos - Ex. P5
Para um aço inoxidável - Mo (Figura ), estime o tempo de vida até a ruptura para um componente que está submetido a uma tensão de () a .
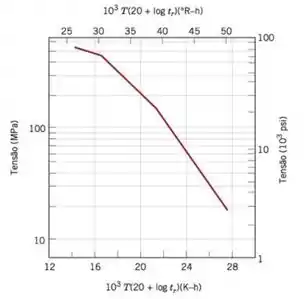
Figura Logaritmo da tensão em função do parâmetro de Larson-Miller para um aço inoxidável - Mo.
Passo 1
Olá! Tudo bem? Esse problema pede que determinemos, para um aço inoxidável - Mo, o tempo de vida até a ruptura para um componente que está submetido a uma tensão de () a . Na Figura , o valor do parâmetro Larson-Miller a é de cerca de , para em e em . Portanto,
Isolando , temos
Resposta
.
Exercícios de Livros Relacionados
Determine a temperatura aproximada na qual a deformação por fluência se torna uma consideração importante para cada um dos seguintes metais: níquel, cobre, ferro, tungstênio, chumbo e alumínio.
Os seguintes dados de fluência foram obtidos para uma liga de alumínio à 400 ° C750 ° F sob uma tensão constante de 25M P a 3660p s i . Trace um gráfico mostrando os dados em termos da deformação em f
Se um componente fabricado da liga S- 590 F i g u r a8.3 0 deve ser exposto a uma tensão de tração de 300M P a 43.500p s i a 650 ° C 1200 ° F , estime seu tempo de vida até a ruptura.
Um corpo de provas com 750m m 30i n de comprimento feito em uma liga S - 590 (Figura 8.31 ) deve ser exposto a uma tensão de tração de 80M P a 11.600p s i , a 815 ° C 1500 ° F . Determine seu alongame
Qual é a carga de tração necessária para produzir um alongamento total de 145m m 5,7i n após 2000h a 730 ° C 1350 ° F para um corpo de provas cilíndrico da liga S- 590 F i g u r a8.31 , originalmente