(a) Considerando o método da interseção, determine o tamanho médio de grão, em milímetros, da amostra cuja microestrutura está mostrada na Figura ; use pelo menos sete segmentos de linhas retas.
(b) Estime o número do tamanho de grão ASTM para esse material.
Passo 1
Olá! Tudo bem? Primeiro responderemos o item (a), neste passo, e (b) no Passo .
(a) Podemos resolver este exercício de duas maneiras: utilizando o software ImageJ ou outro software semelhante, o qual poderá nos dar a informação quanto ao tamanho médio dos grãos por meio de uma medida direta; ou traçando linhas em seu livro texto (versão física), as quais nos darão uma dimensão em centímetros. Após isso, calcularemos a dimensão real em micrometros. Entretanto, optaremos por resolver com o método utilizando o livro texto para traçar as linhas com uma régua, veja:
Devemos traçar retas, com cm de comprimento cada. Devemos ter algo parecido com o que a figura a seguir mostra.
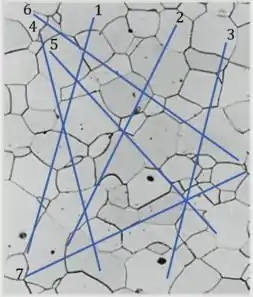
Agora, devemos contar quantos grãos são atravessados por cada reta. Após a contagem, seria indicado organizar os valores em uma tabela, veja:

Após calcularmos a média aritmética do número de grãos interceptados pelas retas, teremos o valor de , o qual usaremos para calcular o comprimento médio de cada grão. Veja:
Agora, devemos relacionar com a escala indicada na Figura . Então temos:
Passo 2
(b) Neste item, devemos saber que o número médio do tamanho de grão, , é relacionado ao número de grãos por polegada quadrada, , com ampliação de , de acordo com a equação Na medida em que a ampliação é de , o valor de é medido diretamente a partir da micrografia. Na micrografia mostrada abaixo foi construído um quadrado com lado de polegada. Portanto, devemos fazer semelhante em nosso livro físico.

O número total de grãos completos dentro deste quadrado é de aproximadamente (considerando as frações de grãos). Agora, para resolver na Equação , é necessário primeiro tomar os logaritmos como:
Resposta
(a)
(b)