Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 7.Perguntas e Problemas - Ex. 30

Um corpo de prova cilíndrico de cobre trabalhado a frio possui uma ductilidade (%Cu) de 25%. Se o seu raio após o trabalho a frio é de 10 mm (0,40 pol.), qual era o seu raio antes da deformação.

Passo 1

Então galera, primeiramente devemos definir a fórmula que usaremos. Precisamos determinar o raio da amostra de cobre. Se liga aí!.

% C u = π r 2 i - π r ² d π r ² i × 100

Nós sabemos que o raio depois do trabalho a frio é de: 10 mm (rd), então temos que achar o raio inicial (ri), para isso devemos isolar na equação:

Vem comigo:

π r ² i = π r 2 i - π r ² d % C u × 100

π r i = π r 2 i - π r ² d % C u × 100

Tirando a raiz dos raios “r²” sobrará apenas o r, e podemos simplificar os “ π "

π r i = π ( r i - r d ) 1 - % C u / 100  

r i = r d 1 - % C u / 100

Passo 2

Agora que isolamos podemos substituir pelos valores fornecidos, porém antes olhem comigo este gráfico:

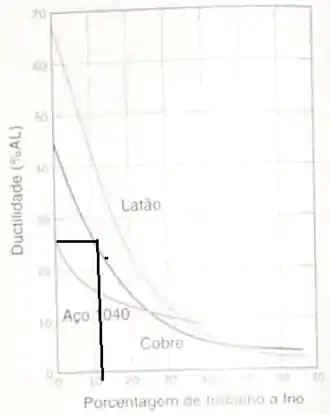
Notem que para 25% de ductilidade temos 11% de trabalho a frio, onde iremos substituir na equação:

r i = 10   m m 1 - 11 / 100

r i = 10,6   m m

Resposta

r i = 10,6   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois corpos de provas cilíndricos de uma liga, previamente sem deformação, devem ser encruados pela redução das áreas das suas seções transversais (embora mantenham as formas circulares das suas seçõe
Dois corpos de provas de um mesmo metal, previamente sem deformação, devem ser deformados plasticamente pela redução das áreas das suas seções transversais. Um dos corpos de provas possui seção transv
a Para um ensaio de tração, mostre que % T F = ϵ ϵ + 1 × 100 Se não houver qualquer alteração no volume do corpo de provas durante o processo de deformação (isto é, se A 0 l 0 = A d l d ). ( b ) Consi
(a) Qual é a ductilidade aproximada (% AL) de um latão que possui um limite de escoamento de 275 MPa (40.000 psi)?(b) Qual é a dureza Brinell aproximada de um aço 1040 que possui um limite de escoamen
Foi observado experimentalmente para os monocristais de diversos metais que a tensão cisalhante rebatida crítica, τ t c r c é função da densidade de discordâncias ρ d segundo a relação τ t c r c = τ o