Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 7.Perguntas e Problemas - Ex. 27
Para um ensaio de tração, mostre que
Se não houver qualquer alteração no volume do corpo de provas durante o processo de deformação (isto é, se ).
Considerando o resultado do item , calcule a porcentagem de trabalho a frio sofrido por um latão naval (cujo comportamento tensão-deformação está mostrado na figura ) quando uma tensão de é aplicada.
Passo 1
Temos, da equação que
O que também podemos expressar como
Temos ainda que pela conservação de volume mencionada no enunciado . Agora, a partir da definição de deformação de engenharia (equação do capítulo anterior) temos
Se substituirmos na expressão da taxa de trabalho a frio vamos ter
Como queríamos demonstrar.
Passo 2
Agora, para resolvermos o segundo item vamos precisar da figura que é dada por
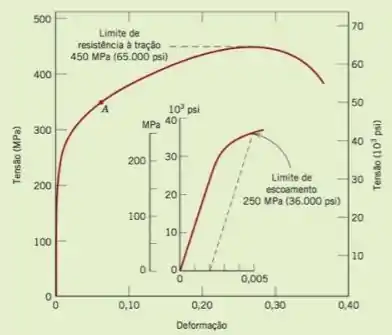
Dela tiramos que uma tensão de corresponde a uma deformação de . Sendo assim, substituindo os valores na expressão dada no item anterior vamos obter