Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 6.Perguntas e Problemas - Ex. 21
Um corpo de provas metálico de formato cilíndrico e com 12,7 mm (0,5 in) de diâmetro e 250 mm (20 in) de comprimento deve ser submetido a um tensão de tração de 28 Mpa (4.000 psi). Nesse nível de tensão, a deformação resultante será totalmente elástica.
- Se o alongamento deve ser inferior a 0,080 mm ( in), quais dos metais na tabela são candidatos adequados? Por quê?
- Se, além disso, a máxima redução permissível no diâmetro for mm ( in) quando a tensão de tração de 28 Mpa for aplicada, quais dos mateis que satisfazem o critério da parte (a) são candidatos adequados? Por quê?
Passo 1
Pra resolver a letra a, a gente vai precisar usar a relação que descreve o gráfico da deformação elástica:
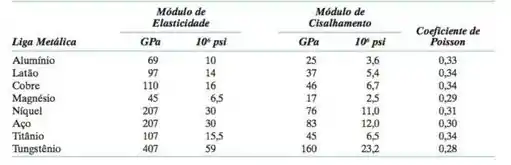
Onde E é o módulo de elasticidade e é a deformação. Usando a tensão de tração e a deformação máxima, chegaremos no módulo de elasticidade máximo. Com esse dado, podemos escolher da tabela todos os materiais que tiverem módulo de elasticidade menor que o máximo como candidatos adequados.
Mas antes, temos que saber a expressão para a deformação:
Pra resolver a letra b, a gente vai precisar relacionar a deformação lateral (do diâmetro) e a deformação axial (do comprimento). Pra isso a gente usa o coeficiente de Poisson :
Usando as deformações máximas, chegaremos no coeficiente de Poisson máximo pro material. Com isso, podemos escolher dentre os materiais, aqueles que possuem o coeficiente dentro do permitido como candidatos adequados.
Passo 2
Primeiro, vamos calcular então a deformação:
Passo 3
Finalmente vamos calcular o módulo de deformação da letra a:
Na tabela os materiais que atendem essa condição são Alumínio e Magnésio.
Passo 4
Antes de calcularmos o coeficiente de Poisson, temos que calcular a deformação lateral!
Agora vamos calcular o coeficiente de Poisson máximo!
Dos materiais apropriados para a letra a, apenas o magnésio atende as condições da letra b.
Resposta
- Alumínio e Magnésio, pois seus módulos de elasticidade atendem a condição de alongamento máximo.
- Magnésio, pois seu coeficiente de Poisson é pequeno o suficiente para a especificação desejada.