Determine os índices de Miller para os planos mostrados na seguinte célula unitária:
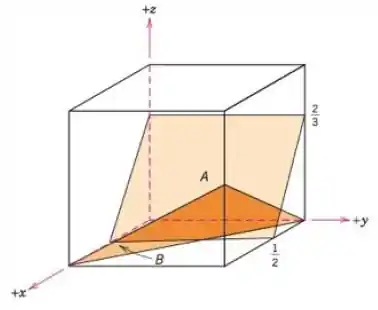
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Temos as seguintes etapas para os índices de Miller:
- Encontrar onde o plano intercepta os eixos.
- Inverter os valores do índice
- Reduzir ao mínimo inteiro os valores obtidos.
Para o plano , temos que:
Ele intercepta o eixo em , é paralelo ao eixo , ou seja, eles só se encontram no infinito e intercepta o eixo em .
Temos que inverter seus valores:
Pra reduzir pra número inteiros só precisamos multiplicar por 2:
Passo 2
O plano já é um pouco mais difícil de visualizar. Temos que considerar um sistema de coordenadas secundário pois uma das interceptações planas com o eixo está ausente. Vamos imaginar que o nosso eixo z está agora na areta azul.
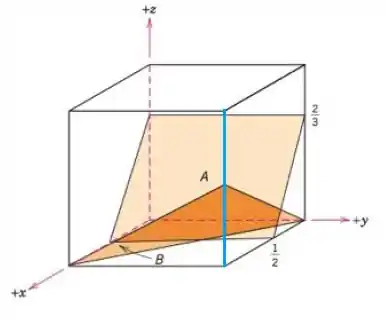
Ele intercepta o eixo em , intercepta o eixo em e intercepta o eixo em .
Invertendo os valores:
Que já é sua forma reduzida.
Resposta
Plano A
Plano B