1. Desenvolva expressões para a densidade planar em termos do raio atômico R para as direções (100) e (111) na estrutura CFC.
2. Calcule e compare os valores da densidade planar para essas mesmas duas direções no níquel.

Letra a:

Na figura abaixo é mostrado um plano (100) para uma célula unitária da CFC.

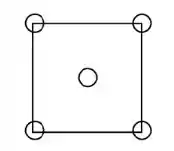
Para este plano (100), há um átomo em cada um dos quatro cantos do cubo, cada um dos quais é compartilhado com quatro células unitárias adjacentes, enquanto o átomo central fica inteiramente dentro da célula unitária. Assim, existe a equivalência de 2 átomos associados a este plano CFC (100). A seção plana representada na figura acima é um quadrado, em que os comprimentos laterais são iguais ao comprimento da aresta da célula unitária, (Equação 3.1); e, portanto, a área desse quadrado é apenas . Portanto, a densidade planar para este (100) plano é apenas:

A porção de um plano CFC (111) contida em uma célula unitária é mostrada abaixo:

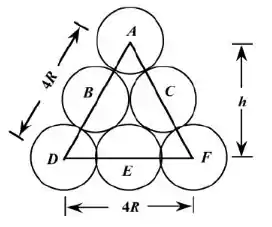
Existem seis átomos cujos centros estão neste plano, rotulados de A a F. Um sexto de cada um dos átomos A, D e F está associado a este plano (produzindo uma equivalência de meio átomo), com um metade de cada um dos átomos B, C e E (ou uma equivalência de um e meio átomos) para uma equivalência total de dois átomos. Agora, a área do triângulo mostrada na figura acima é igual à metade do produto do comprimento da base e da altura, h. Se considerarmos metade do triângulo, então:

O que leva a . Assim, a área é igual a:

E, portanto, a densidade planar é: