Determine as tensões de trabalho para as duas ligas cujos comportamentos tensão-deformação estão mostrados nas Figuras e .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
A tensão de trabalho é dada pela equação:
Onde:
Observe a figura , que indica o comportamento tensão-deformação para o latão:
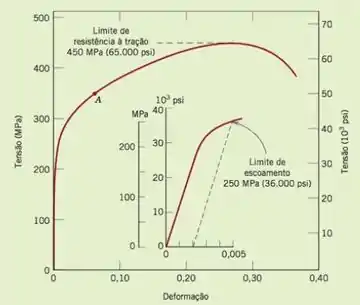
Para o latão, podemos observar que o limite de escoamento é de:
Passo 2
O valor do fator de segurança não é mencionado na pergunta. Este fator depende de muitos fatores, como propriedades do material, forças mecânicas e etc.
Geralmente, a faixa de está entre e . Vamos considerar um fator de segurança de:
Portanto:
A tensão de trabalho para o latão será de:
Passo 3
Observe a figura , que indica o comportamento tensão-deformação para o aço:
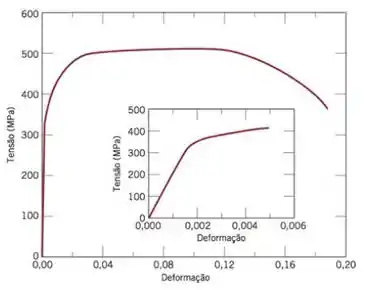
Como na imagem não é informado o valor do limite de escoamento temos que fazer uma linha de compensação de deformação em . Ela deve ter a mesma inclinação da linha que representa a região elástica:
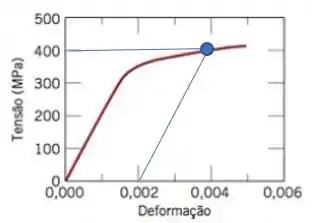
Podemos observar que o limite de escoamento é de aproximadamente:
Passo 4
Podemos utilizar o mesmo fator de segurança de:
Portanto:
A tensão de trabalho para o latão será de:
Resposta
Para o latão da Figura a tensão de trabalho é de:
Para o aço da Figura a tensão de trabalho é de: